[科普中国]-指数函数

基本概念

细胞的分裂是一个很有趣的现象，新细胞产生的速度之快是十分惊人的。例如某种细胞在分裂时，1个分裂成2个，2个分裂成4个……第x次分裂得到新细胞数y与分裂次数x的函数关系式： 。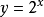

这个函数是幂的形式，且自变量为幂指数，我们下面来研究这样的函数。

一般地，函数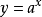 (a为常数且以a>0，a≠1)叫做指数函数，函数的定义域是R。2对于一切指数函数来讲，值域为(0， +∞)。

指数函数中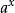 前面的系数为1。如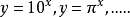： 都是指数函数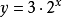； 不是指数函数。2

数学术语指数函数是数学中重要的函数。应用到值e上的这个函数写为exp(x)。还可以等价的写为ex，这里的e是数学常数，就是自然对数的底数，近似等于 2.718281828，还称为欧拉数。

当a>1时，指数函数对于x的负数值非常平坦，对于x的正数值迅速攀升，在 x等于0的时候，y等于1。当00且a≠1。

基本性质如图所示为a的不同大小影响函数图形的情况。

在函数中可以看到 ：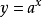

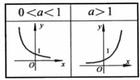
（1） 指数函数的定义域为R，这里的前提是a大于0且不等于1。对于a不大于0的情况，则必然使得函数的定义域不连续，因此我们不予考虑，同时a等于0函数无意义一般也不考虑。

（2） 指数函数的值域为(0， +∞)。

（3） 函数图形都是上凹的。

（4） a>1时，则指数函数单调递增；若0