[科普中国]-有限覆盖定理

简介

有限覆盖定理：设H是闭区间[a,b]的一个（无限）开覆盖，则必可以从H中选择有限个开区间来覆盖[a,b]1。

有限覆盖定理是一个有用而且重要的定理．它是数学分析处理问题的一种重要方法，在数学各领域中都有广泛的应用．有限覆盖定理的作用是从覆盖闭区间的无限个开区间中能选出有限个开区间也覆盖这个闭区间．由“无限转化为有限”是质的变化，它对证明函数的某些性质提供了新的数学方法2。

定律定义在讲有限覆盖定理之前，先介绍覆盖的概念。

覆盖：设有任意个区间（可以是开区间，也可以是闭区间，还可以是半开半闭区间；可以是有限个区间，也可以是无限个区间），它们构成了一个集合H（集合H的所有元素均为区间）。如果对于一个数集S，S中的任意一个元素都属于H中的至少一个区间，那么称H是S的一个覆盖。

它的等价定义为，若S包含于任意个区间所构成的并集，则称这些区间构成的集合H是S的一个覆盖。

特别地，当H中的元素全部为开区间时，称H是S的开覆盖。

例如，数集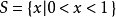 ，它的一个覆盖为 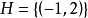。这是因为，对任意0