[科普中国]-高斯消元法

简介

数学上，高斯消元法（或译：高斯消去法），是线性代数规划中的一个算法，可用来为线性方程组求解。但其算法十分复杂，不常用于加减消元法，求出矩阵的秩，以及求出可逆方阵的逆矩阵。不过，如果有过百万条等式时，这个算法会十分省时。一些极大的方程组通常会用迭代法以及花式消元来解决。当用于一个矩阵时，高斯消元法会产生出一个“行梯阵式”。高斯消元法可以用在电脑中来解决数千条等式及未知数。亦有一些方法特地用来解决一些有特别排列的系数的方程组。

历史该方法以数学家高斯命名，由拉布扎比.伊丁特改进，发表于法国但最早出现于中国古籍《九章算术》，成书于约公元前150年。1

原理内容消元法是将方程组中的一方程的未知数用含有另一未知数的代数式表示，并将其代人到另一方程中，这就消去了一未知数，得到一解；或将方程组中的一方程倍乘某个常数加到另外一方程中去，也可达到消去一未知数的目的。消元法主要用于二元一次方程组的求解。

核心1)两方程互换，解不变；

2)一方程乘以非零数k，解不变；

3)一方程乘以数k加上另一方程，解不变2。

求逆矩阵具体例子例如，考虑下面的矩阵

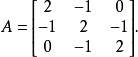
为了找到这个矩阵的逆矩阵，扩充以下矩阵：

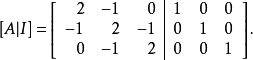通过计算，可以将增广矩阵转换为简化行阶梯形式，即把左边转化为单位矩阵：

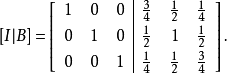
求得B为A的逆矩阵。

其他应用找出逆矩阵高斯消元法可以用来找出一个可逆矩阵的逆矩阵。设A 为一个N * N的矩阵，其逆矩阵可被两个分块矩阵表示出来。将一个N * N单位矩阵 放在A 的右手边，形成一个N * 2N的分块矩阵B = [A,I] 。经过高斯消元法的计算程序后，矩阵B 的左手边会变成一个单位矩阵I ，而逆矩阵A ^(-1) 会出现在B 的右手边。

假如高斯消元法不能将A 化为三角形的格式，那就代表A 是一个不可逆的矩阵。

应用上，高斯消元法极少被用来求出逆矩阵。高斯消元法通常只为线性方程组求解。

计出秩的基本算法高斯消元法可应用在任何m * n的矩阵A。在不可减去某数的情况下，我们都只有跳到下一行。以一个6 * 9的矩阵作例，它可以变化为一个行梯阵式：

1 * 0 0 * * 0 * 0

0 0 1 0 * * 0 * 0

0 0 0 1 * * 0 * 0

0 0 0 0 0 0 1 * 0

0 0 0 0 0 0 0 0 1

0 0 0 0 0 0 0 0 0

而矩阵中的 *' 是一些数字。这个梯阵式的矩阵T 会有一些关于A的资讯：

A 的秩是5，因为T 有5行非0的行；

A 的列的向量空间，可从A 的第1、3、4、7和9列中得知，其数值在矩阵T 之中；

矩阵中的 *' 表示了A 的列可怎样写为列中的数的组合。1

分析高斯消元法的算法复杂度是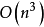；这就是说，如果系数矩阵的是n × n，那么高斯消元法所需要的计算量大约与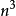成比例。

高斯消元法可用在任何域中。

高斯消元法对于一些矩阵来说是稳定的。对于普遍的矩阵来说，高斯消元法在应用上通常也是稳定的，不过亦有例外。1

伪代码高斯消元法的其中一种伪代码:

i=1j=1while(i≤mandj≤n)doFind pivot in column j,starting in row i:maxi:=ifork:=i+1tomdoifabs(A[k,j])>abs(A[maxi,j])thenmaxi:=kendifendforifA[maxi,j]≠0thenswap rows i and max i,but do not change the value of iNow A[i,j]will contain the old value of A[maxi,j].divide each entry in row i by A[i,j]Now A[i,j] will have the value 1.foru:=i+1tomdosubtractA[u,j]*rowifromrowuNowA[u,j]willbe0,sinceA[u,j]-A[i,j]*A[u,j]=A[u,j]-1*A[u,j]=0.endfori=i+1endifj=j+1endwhileoutput subtractA[u,j]这个算法和之前谈及的有点儿不同，它由绝对值最大的部分开始做起，这样可以改善算法上的稳定性。将经过调换后的第一列作为起点，这算法由左至右地计算。每作出以下两个步骤，才跳到下一列：

1.定出每列的最后一个非0的数，将每行的数字除以该数，使到每行的第一个数成为1；

2.将每行的数字减去第一行的第一个数的某个倍数。

所有步骤完成后，这个矩阵会变成一个行梯阵式，再用代入法就可解决这个方程组。

线性方程组其实是相当容易解决的，基本的思想就是消元。但是当未知数较多时，解起来也蛮头疼的。在这里向大家介绍高斯消元法。例如解如下四元一次方程组：

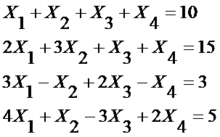
除去各未知数，将各数排在一起，成为矩阵：

为方便起见，用r2+r1表示把第一行各数加到第二行对应数上。

r2-2*r1, r3-3*r1, r4-4*r1,r3+4*r2, r4+3*r2,r4-2*r3, 可得：

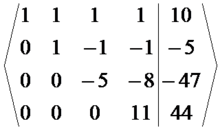
化为方程组形式则为：

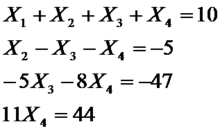
从而，可得：

X4=4

X3=3

X2=2

X1=1.

说明：对于矩阵采取的变换的合理性，可对照相应方程组的变换加以理解。1