[科普中国]-极大值

定义

一般的，设函数f(x)在点x0附近有定义，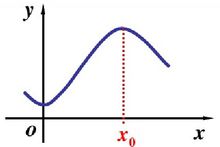

（1）如果对x0附近的所有点，都有f(x)f(x0)，则f(x0)是函数f(x)的一个极小值，如图2所示；

（3）函数的极大值与极小值统称为极值。(极值即波峰波谷处的值——不一定是最大值或最小值)

（4）使得函数取得极值的点x0称为极值点。使得函数取得极大值的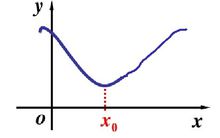点x0称为极大值点；使得函数取得极小值的点x0称为极小值点。

极大值和最大值的区别最大值是函数中最大的值，而极大值不是。

最大值一定高于函数中其他的值，极大值可以小于极小值。

最大值的值只有一个，而极大值的值可以有无限个。

最大值的定义区间为函数定义域，极大值可以自定义区间。

注意需要注意以下几点：

（1）极大值、极小值是一个局部概念。由定义，极大值、极小值只是某个点的函数值与它附近点的函数值比较是最大或最小，并不意味着它在函数的整个的定义域内最大或最小，因此，极大值、极小值不同于最大值、最小值。

（2）函数的极值不是唯一的，即一个函数在某区间上或定义域内极大值或极小值可以不止一个。

（3）极大值与极小值之间无确定的大小关系，即一个函数的极大值未必大于极小值，极小值也未必小于极大值。

（4）函数的极值点一定出现在区间的内部，区间的端点不能成为极值点，而使函数取得最大值、最小值的点可能在区间的内部，也可能在区间的端点。

求极大值的方法对于单变量函数，有如下求极大值的方法。

对于连续可导的函数（1）一阶导数判别法：

对于可导函数f(x)，判别f(x)是否有极大值的步骤如下：

1）求导数 f′(x)；

2）求 f(x)的驻点，即求 f′(x)=0 的根；

3）检查 f′(x)在驻点左右的符号，如果在驻点左侧附近为正，右侧附近为负，那么函数y=f(x)有极大值，且在这个驻点处取得极大值；否则，函数f(x)无极大值。

（2）二阶导数判别法（函数二阶可导）

已知f(x)在x0的某邻域上一阶可导，在x0处二阶可导，且f'(X0)=0，f"(x0)≠0，那么：

1）若f"（x0）