研究历史
复分析中的柯西-黎曼微分方程是提供了可微函数在开集中全纯函数的充要条件的两个偏微分方程,以柯西和黎曼得名。这个方程组最初出现在达朗贝尔的著作中(d'Alembert 1752)。后来欧拉将此方程组和解析函数联系起来(Euler 1777)。 然后柯西(Cauchy 1814)采用这些方程来构建他的函数理论。黎曼关于此函数理论的论文(Riemann 1851)于1851年问世。
方程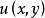 在一对实值函数
在一对实值函数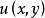 和
和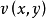 上的柯西-黎曼方程组包括两个方程:
上的柯西-黎曼方程组包括两个方程:
(1)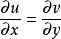
(2)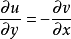
柯西-黎曼方程是函数在一点可微的必要条件。
设函数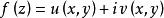 在区域D内有定义,则它在D内解析的充分必要条件是:
在区域D内有定义,则它在D内解析的充分必要条件是:
1)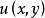 与
与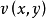 在D内处处可微;
在D内处处可微;
2)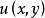 与
与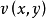 在D内处处满足一阶偏微分方程组
在D内处处满足一阶偏微分方程组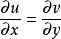 ,
,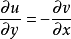 。1
。1
证明过程设函数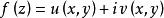 定义在区域D内,并在D内一点
定义在区域D内,并在D内一点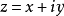 可导(或可微),于是
可导(或可微),于是
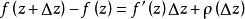 式中,
式中,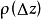 满足
满足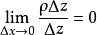 .
.
其中
 则
则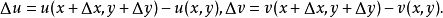
代入式
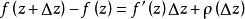
并比较实部和虚部得
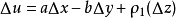
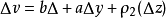
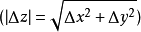
由于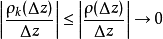
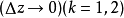 ,
,
因此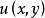 及
及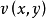 在点
在点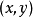 可微,并且成立
可微,并且成立
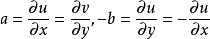 方程
方程
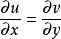 ,
,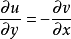
称为柯西-黎曼(Cauchy-Riemann)方程,简称C-R方程。
这就得到了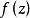 在点z可导的必要条件。实际上,这个条件也是充分的,以下证明充分性。
在点z可导的必要条件。实际上,这个条件也是充分的,以下证明充分性。
设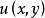 ,
,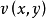 在点
在点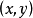 可微,则有
可微,则有
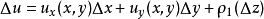
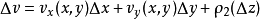
于是由C-R方程得
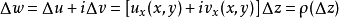
其中,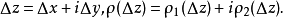
由于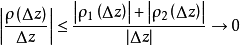
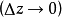 ,
,
因此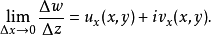
即函数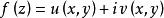 在
在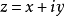 可导。
可导。
由以上讨论可知,当定理的条件满足时,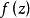 在点z的导数为:
在点z的导数为:
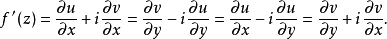




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国