[科普中国]-矩阵函数

定义

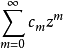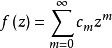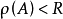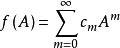设复变幂级数的收敛半径是R，且在收敛域内，当矩阵A的谱半径，定义，并称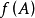为矩阵A的函数1。

常用的矩阵函数（1）矩阵指数函数：对于任意A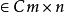 ，有：

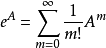
（2）正弦函数，是一种矩阵三角函数：对于任意A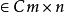，有：

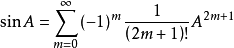
（3）余弦函数，是一种矩阵三角函数：对于任意A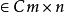，有：

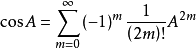
定理1、定理1：假设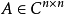，则有：

（1）；

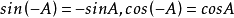（2）。

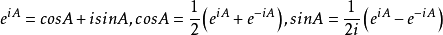注意：因为矩阵的乘法不满足交换律， 因此矩阵函数不一定满足一般函数的所有性质。

2、定理2：设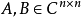，且AB=BA，则有：

（1）；

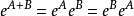（2）；

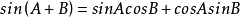（3）。

3、根据定理 2 ，很容易证得下面结论：

推论 ：设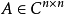，则有：

（1）；

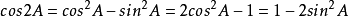（2）；

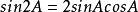（3）。

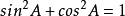求解矩阵函数的方法利用矩阵标准型用矩阵标准型求矩阵函数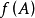的具体步骤如下：

（1）设方阵A相似于对角阵，即

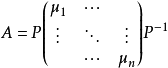
，其中矩阵内的值是A的n个特征值，则

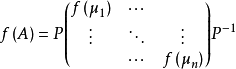
（2）当A不能与对角阵相似时，则A必与Jordan标准型相似，设

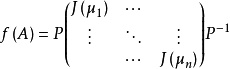
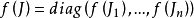
最后

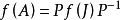
利用最小多项式用最小多项式求矩阵函数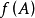的具体步骤如下：

第一步 计算矩阵A的最小多项式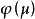，确定其次数m及特征值；

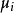第二步 设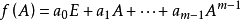，确定出系数；

第三步 代入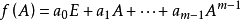可求得。