[科普中国]-完全四边形

定义

把两两相交又没有三线共点的四条直线及它们的六个交点所构成的图形，叫做完全四边形。六个点可分成三对相对的顶点，它们的连线是三条对角线。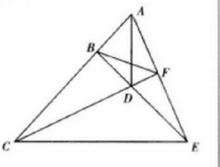

如图一，直线ABC、BDE、CDF、AFE两两相交于A、B、C、D、E、F六点，即为完全四边形ABCDEF。线段AD、BF、CE为其三条对角线。

完全四边形中既有凸四边形、凹四边形、还有折四边形以及四个三角形。如图一中有凸四边形ABDF、凹四边形ACDE、还有折四边形BCFE，以及四个三角形△ACF、△BCD、△DEF、△ABE。2

基本概念设A、B、C、D是位于同一平面上的四个点，其中任何三点都不共线，则由六条线段AB、CD、AC、BD、AD、BC所构成的图形，称为完全四角形。这四个点称为完全四角形的顶点，而这六条线段称为完全四角形的边。不通过同一顶点的三组边AB与CD，AD与BC，AC与BD，称为对边；对边的交点P、Q、R称为对角点；以对角点为顶点的三角形，称为对角三角形。在完全四角形中，通过两个对角点的直线与不通过这两个对角点的一组对边的交点，同所给两个对角点一起构成一个调和点列。基于上述事实，当在直线上给定两个点P、R时，就能作出该直线上任意点X关于点P、R的调和共轭点Y。作图方法如下：

(1)任取不在直线PR上的点A。

(2)引直线AP、AR、AX。

(3)在AP上任取点B，引直线BR，设BR与AX的交点为C。

(4)设直线PC与AR的交点为D。

(5)作直线BD与PR的交点Y。Y就X关于点P、R的调和共轭点。3

性质1.完全四边形的一条对角线被其他两条对角线调和分割(两点内分与外分间一线段成同一比值，称这两点调和分割这一线段)。

2.过完全四边形对角线所在直线的交点作另一条对角线的平行线，所作直线与平行对角线的同一端点所在的边(或其延长线)相交，所得线段被此对角线所在直线的交点平分。

3.在完全四边形ABCDEF中，四边形ABDF有内切圆的充分必要条件是△ACD与△ADE的内切圆相外切。

4.完全四边形ABCDEF的三条对角线AD、BF、CE的中点M、N、P共线（即牛顿线）。

5.完全四边形的三条对角线为直径的圆共轴，且完全四边形的四个三角形的垂心在这条轴上。

6.完全四边形的垂足线与牛顿线垂直(两圆连心线垂直于公共弦)。

7.完全四边形的四个三角形的外接圆圆心共圆．这四个圆心每三个构成的三角形的垂心分别在构成完全四边形的四条直线上，且这四个垂心为顶点构成的四边形与四个圆心为顶点构成的四边形全等。2

8.在完全四边形ABCDEF中，四边形ABDF(在∠BAF内)有旁切圆的充分必要条件是下列两条件之一：

1)AB+BD=AF+FD；2)AC+CD=AE+ED。4