[科普中国]-玫瑰线

简介

玫瑰线的说法源于欧洲海图。在中世纪的航海地图上，并没有经纬线，有的只是一些从中心有序地向外辐射的互相交叉的直线方向线。此线也称罗盘线，希腊神话里的各路风神被精心描绘在这些线上，作为方向的记号。葡萄牙水手则称他们的罗盘盘面为风的玫瑰（rosedosventor）。水手们根据太阳的位置估计风向，再与“风玫瑰”对比找出航向。玫瑰线，即指引方向的线。

历史世界上第一个明确提出经纬度理论的人是古希腊学者托勒密。最早的本初子午线则出现在15世纪出版的托勒密的世界地图上，定在了当时人们心中的世界起点，即现大西洋中非洲西北海岸附近的加那利群岛。

不像纬线有长 有短，所有经线的长度皆相同，人们可以选择通过地球上任何一点的经线作为起始线。于是，在过去的许多年里，每个国家出版的地图所用经度皆是由自己的起始经线进行推算的，而航海家们使用的航海地图又往往是采用某一航线的出发点作为起算点。巴黎零度经线的设立比格林尼治线要早，不过无论是巴黎经线还是格林尼治经线，这些零度经线的划定都是主观的划定。

应用1569年墨卡托发明了航海图沿用至今的投影，不过绘有经纬网的世界地图30年后才得以出版，零度经线设在大西洋上的亚速尔群岛。那时英国所使用的航海图，零度经线也设在亚速尔群岛。

1676年改为伦敦，最初定点在圣保罗大教堂，后定点在格林尼治天文台。

1634年在法国，红衣主教里舍利厄选中了通过加那利群岛最西边的耶鲁岛的经线作为零度经线。

1667年巴黎天文台建立，零度经线改为通过巴黎的经线。

17世纪荷兰地图上，零度经线是阿姆斯特丹威斯特教堂的南北轴。西班牙以西、葡分界的教皇子午线为零度经线。意大利地图上使用的零度经线位于罗马。

清康熙四十八年在中国，清政府确定了京城中轴线为零度经线。

1675年当精确测定经度成为航海的关键问题后，英国在伦敦附近建立了格林尼治天文台，并第一个研究出了简易测定航海中船舶方位的方法。

1767年根据格林尼治天文台提供的数据绘制的英国航海历出版，这份航海历上的零度经线就是通过格林尼治天文台的经线。这个时候的英国，已是头号海上强国。

1850年美国政府决定在航海图中采用格林尼治子午线取代通过华盛顿的零度经线作为本初子午线。

1853年俄国海军宣布不再使用普尔可夫天文台(今列宁格勒附近)的零度经线编制航海历，而采用格林尼治子午线为本初子午线。

1883年可以说除了法国编制的地图，其余国家的地图几乎都是采用格林尼治经线作为零度经线。

更名1884年，国际子午线会议在美国华盛顿召开，通过决议把经过格林尼治的经线正式确定为零度经线、世界时间计量和经度计量的标准子午线――本初子午线。不过法国人并不服气这个决议，在自己国家发行的地图上，仍将本初子午线定在首都巴黎，直到1911年后才改为格林尼治线。可见，对于事实，大家并不一定有共识，而是依赖自己的观点而定.

至今，玫瑰线在英国的格林威治。但过去并非如此。

在将格林威治天文台确定为本初子午线所经过的一点之前，零度经线正好穿过巴黎，穿过圣舒尔皮斯教堂。圣舒尔皮斯教堂的铜线是为了纪念全世界第一条本初子午线的。虽然，格林威治于1888年从巴黎手中夺走了这项殊荣，但当初的玫瑰线依然可见。

数学中的玫瑰线方程及其几何结构玫瑰线的极坐标方程为:ρ=a* sin(nθ),ρ=a*cos(nθ)

用直角坐标方程表示为: x=a* sin(nθ)* cos(θ), y=a*sin(nθ)* sin(θ)

根据三角函数的特性可知,玫瑰线是一种具有周期性且包络线为圆弧的曲线,曲线的几何结构取决于方程参数的取值,不同的参数决定了玫瑰线的大小、叶子的数目和周期的可变性。这里参数a(包络半径)控制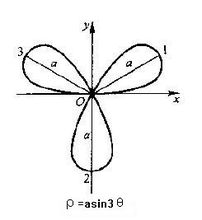叶子的长短,参数n控制叶子的个数、叶子的大小及周期的长短。

如对于方程式ρ=5* sin(3*θ)、ρ=5* sin(2*θ)、ρ=5* sin(3*θ/2)，分别对应的是三叶、四叶和六叶玫瑰线。

玫瑰线总面积A

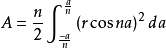a = π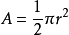

玫瑰线的参数特性玫瑰线的参数主要是a、n及θ,其值的大小决定玫瑰线的形状,包括叶子数、叶子长度宽度和曲线闭合周期。系数a只跟叶子的长度有关,而n和θ则影响玫瑰线的多样性和周期性,本文主要讨论n和θ对玫瑰线几何结构的影响,从而揭示玫瑰线的生成规则。通过计算机对方程式ρ=a* sin(nθ)的大量试验,证明玫瑰线具有如下三个特性:

特性1 当n为整数时,若n为奇数,则玫瑰线的叶子数为n,闭合周期为π,即θ角在0-π内玫瑰线是闭合的。当n为偶数时,玫瑰线的叶子数为2n,闭合周期为2π,即θ角取值在0-2π内玫瑰线才是闭合和完整的。

特性2 当n为非整数的有理数时,设为L/W,且L/W为简约分数,此时,L与W不可能同时为偶数。L决定玫瑰线的叶子数,W决定玫瑰线的闭合周期(Wπ或2Wπ,见特性3)及叶子的宽度,W越大,叶子越宽。但W也会同时影响叶子数的多少,对同一奇数值L,在W分别取奇数和偶数值时,叶子数也是不同的。

特性3 当L或W中有一个为偶数时,玫瑰线的叶子数为2L,闭合周期为2Wπ。当L或W同为奇数时,玫瑰线的叶子数为L,闭合周期为Wπ。换句话说,生成偶数个叶子的玫瑰线, L或W中必须有且只有一个为偶数值,且L为叶子数的一半,而生成奇数个叶子的玫瑰线, L和W都必须为奇数,且L值就是叶子数。1

玫瑰线的生成规则对于给定叶子数的玫瑰线,可以通过选择n或L/W不同形式来生成。