[科普中国]-模曲线

简介

在数论和代数几何中，模曲线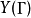 是黎曼表面或相关的代数曲线，通过积分2×2矩阵 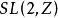的模块化组的子群 ，构造为复上半平面H的商。模曲线也可以用于指压缩模曲线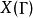 ，它们是通过将有限多个点（称为 的尖点）添加到该商（通过在扩展的复上半平面上）而获得的紧凑化。模曲线的参数以及 群的一些附加特征拟合椭圆曲线的同构类。这个解释给出了模曲线的纯代数而不考虑复数的定义，而且证明了模曲线是在有理场Q上建立的，或者是一个循环场。后一种和它的概括在数论中是根本的重要性。1

分析定义模块化组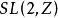 通过分数线性变换作用在上半平面上。 模曲线的分析定义涉及对于某些正整数N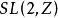， 的同余子群 ，即包含 的同余子群，其中

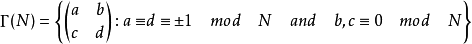
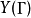N被称为 的水平。可以将 \H上的复杂结构放在通常表示为 的非紧密黎曼表面表面上。2

紧模曲线通过添加有限的称为 的尖点获得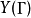 的紧凑化。 具体来说，这是通过扩展复合上半平面 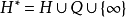上的 来完成的。 以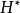 为基础引入拓扑结构：

（1）H的任何开放子集；

（2）对于所有r> 0，集合 ；

（3）对于所有互质整数a，c和所有r> 0， 的像

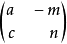
m,n是整数，并且

这使得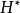 变成作为黎曼球 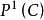的子集的拓扑空间。 组 作用于子集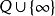 ，将其分解成有限的许多轨道，称为 的尖点。 如果 在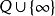 上过渡运行，则空间 \ 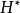成为 \H的Alexandroff压缩。 再次，复数结构可以放在商\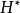上，使其变为表示为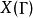的黎曼表面，其现在是紧凑的。 这个空间是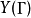的紧凑化。

举例最常见的示例是与子组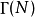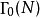，和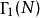相关联的曲线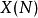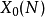，和。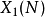

模曲线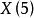具有属性0：它是具有12个尖点的黎曼球，位于常规二十面体的顶点。 X（5）→X（1）通过二次面组在黎曼球体上来实现。 这个组是一个和A5和PSL（2,5）同构的简单组。

模曲线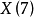是具有24个尖点的3类克莱恩。 它可以解释为具有三个柄的表面，由24个七边形平铺，每个面的中心具有尖点。 这些可以通过dessins d'enfants和Belyi函数来理解，而边缘的顶点和中心（黑色和白色点）是0和1之间的点。X（7）→X（1）的伽罗瓦组是与PSL同构的一个168类的简单组PSL（2,7）。

对于经典模曲线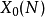，有一个明确的经典模型，有时被称为模曲线。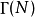的定义可以重述如下：它是作为缩减模N的内核的模块组的子组。然后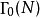是上三角模N的矩阵的较大子组：

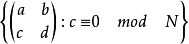
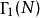是由下式定义的中间体：

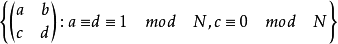
这些曲线具有作为具有水平结构的椭圆曲线的模数空间，并且因此它们在算术几何中起重要作用。 水平为N的模曲线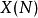是椭圆曲线的模空间。 对于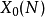和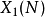，层次结构分别是阶数N和阶N的循环子组。这些曲线已经被非常详细地研究，特别是已知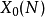可以通过Q定义。

定义模曲线的方程是模方程式中最着名的例子。 “最佳模型”可以与直接从椭圆函数理论得出的结果不同。黑克操作员可以在几何学上进行研究，作为连接成对的模曲线的对应关系。3

型X（N）→X（1）是伽罗瓦，伽罗瓦组SL（2，N）/ {1，-1}，如果N为素数则等于PSL（2，N）。 应用黎曼 - 赫尔维茨公式和高斯 - 博内定理，可以计算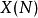的属。 对于素数级≥5，

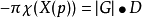
其中是欧拉特征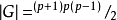，是组PSL（2，p）的顺序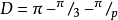，是球（2,3,p）的角。 这产生一个公式

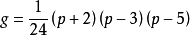
因此，X（5）具有型0，X（7）具有型3，X（11）具有型26。对于p = 2或3，还必须考虑分支，即存在阶数p PSL（2，Z）中的元素以及PSL（2,2）具有型6而不是型3的事实。对于涉及的任何级别N的模曲线X（N）的属来说，存在更复杂的公式 N.的除数。