[科普中国]-共轭方向

基本概念

两向量间的一种特殊关系.设A为n×n对称正定矩阵，向量p，p∈R.若满足条件(p)Ap=0，则称p和p关于A是共轭方向，或称p和p关于A共轭.一般地，对于非零向量组p，p，…，p∈R，若满足条件：(p)Ap=0(i≠j，i，j=1，2，…，n)，则称该向量组关于A共轭。

设A是n×n对称正定矩阵，若有两个n维向量P和Q，满足

PAQ=0

则称向量P和Q是关于A共轭的，或称P、Q是A共轭方向。

定义设A为n阶实对称正定矩阵，如果有两个n维向量S1和S2满足

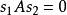（1）

则称向量S1与S2对于矩阵A共轭。如果A为单位矩阵，则式(1)即成为S1S2，这样两个向量的点积（或称内积）为零，此二向量在几何上是正交的，它是共轭的一种特例。

设A为对称正定矩阵，若一组非零向量S1，S2，…Sn满足

SiASj=0 （i≠j） （2）

则称向量系Si（i=1,2，…n）为关于矩阵A共轭。

共扼向量的方向称为共轭方向。1

数学表达设A是n×n对称正定矩阵，若有两个n维向量P和Q，满足

PAQ=0

则称向量P和Q是关于A共轭的，或称P、Q是A共轭方向。

对m个n维向量P，P，…，p，(m