[科普中国]-球面

相应概念

在三维空间、欧几里得、几何学，球面被设定为是在R空间中与一个定点距离为r的所有点的集合，此处r是一个正的实数，称为半径，固定的点称为球心或中心，并且不属于球面的范围。r = 1是球的特例，称为单位球。1

引用公式被球面紧贴包围的立体称为球体，简称球。2在空间直角坐标系中，以坐标原点为球心，半径为R的球面的方程为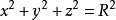，它的参数方程为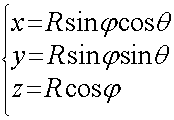（0≤θ≤2π，0≤φ≤π）

在解析几何，球是中心在(x0,y0,z0)，半径是r的所有点(x, y, z)的集合：

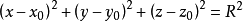
使用极坐标来表示半径为r的球面：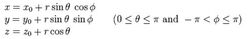

x=x0+r sinθcosφ

y=y0+r sinθsinφ

z=z0+r cosθ

(θ的取值范围：0≤θ≤ n 和 -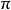0时，表示一球面；当a^2+b^2+c^2-d=0时，表示一点（a,b,c）;当a^2+b^2+c^2-d