[科普中国]-高斯过程

定义

高斯过程指的是一组随机变量的集合，这个集合里面的任意有限个随机变量都服从联合高斯分布1。

性质一个高斯过程完全由它的均值函数和协方差函数决定，只要均值函数m(x)和协方差函数k(x,x')确定了，这个高斯过程也就完全确定了。

高斯过程有很多与高斯变量类似的统计特征，如：

1. 高斯过程通过线性系统或高斯过程的线性组合仍为高斯型。

2. 如果高斯过程是广义平稳的，则等价于平稳。

3. 如果高斯过程的时间进程中两个不同时刻的随机变量不相关，则等价于统计独立1。

4. 高斯过程的线性积分则为相应的高斯随机变量。

在通信系统中，电子器件内部的自由电子的热运动（热噪声），真空电子管的起伏发射和半导体中载流子的非均匀变化（又称散弹噪声，shot ），电源滤波不良的哼哼声等，它们的统计特性基本上都是高斯分布，即高斯过程。

5、两个高斯分布律的随机变量的卷积是高斯分布律，它的均值和方差是原来两个高斯分布律的均值和方差的代数和。

6、高斯过程的边缘似然函数

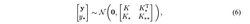
7、高斯过程的条件概率公式

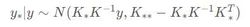
高斯过程的重要性1、广泛性

中心极限定理：大量独立的、均匀微小的随机变量的总和近似地服从高斯分布。

例如，无线电设备中的热噪声（前置放大器）、通信信道中噪声信号、大气湍流、宇宙噪声、维纳噪声（布朗运动）等等。

2、数学优点

二阶矩、广义平稳与狭义平稳等价，高斯随机过程通过线性系统还是高斯随机过程。

应用高斯过程将多元高斯分布扩展到无限维度2。任意数据集中n个观测量，y={y_{1},..,y_{n}}y=y1,..,yn都可以理解成从某个多元高斯分布中抽取的一个样本。高斯过程最重要的应用是解决回归问题3。假设训练集数据为y，新数据为y*，那么我们可以根据高斯过程的性质估计新数据的分布。

例子：假设我们有下图的历史数据：

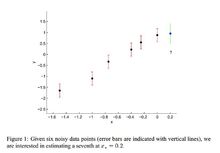
我们要估计新的数据点x*=0.2的分布。根据上述过程，我们首先有6个观测值y，分别是：

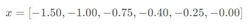
从误差线得知\sigma_{n}=0.3，那么根据协方差公式，我们有：

根据高斯过程的条件概率公式，我们可以计算出新观测点的均值与方差分别是0.95与0.21。即服从N（0.95，0.21）的高斯分布。