[科普中国]-相对熵

定义

相对熵（relative entropy）又称为KL散度（Kullback–Leibler divergence，简称KLD），信息散度（information divergence）。

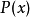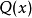设 和 是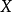 取值的两个离散概率分布，则 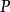对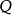 的相对熵为：

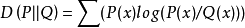
对于连续的随机变量，定义为：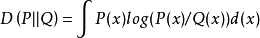

相对熵是两个概率分布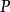 和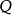 差别的非对称性的度量。1

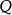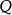物理意义相对熵是用来度量使用基于 的编码来编码来自 的样本平均所需的额外的比特个数。 典型情况下， 表示数据的真实分布， 表示数据的理论分布，模型分布，或 的近似分布。

根据shannon的信息论，给定一个字符集的概率分布，我们可以设计一种编码，使得表示该字符集组成的字符串平均需要的比特数最少。假设这个字符集是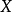 ，对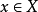 ，其出现概率为 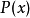，那么其最优编码平均需要的比特数等于这个字符集的熵：

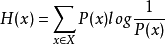
在同样的字符集上，假设存在另一个概率分布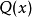 ，如果用概率分布 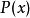的最优编码（即字符 的编码长度等于 ），来为符合分布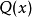 的字符编码，那么表示这些字符就会比理想情况多用一些比特数。相对熵就是用来衡量这种情况下平均每个字符多用的比特数，因此可以用来衡量两个分布的距离，即：

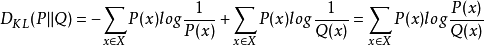
由于对数函数是上凸函数，所以：

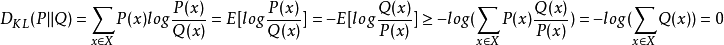
所以相对熵始终是大于等于0的，当且仅当两分布相同时，相对熵等于0。

性质相对熵（KL散度）有两个主要的性质，如下：

（1）不对称性

尽管KL散度从直观上是个度量或距离函数，但它并不是一个真正的度量或者距离，因为它不具有对称性，即

（2）非负性

相对熵的值为非负值，即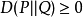 ，证明可用吉布斯不等式。1

区别与联系信息熵，是随机变量或整个系统的不确定性。熵越大，随机变量或系统的不确定性就越大。

相对熵，用来衡量两个取值为正的函数或概率分布之间的差异。

交叉熵，用来衡量在给定的真实分布下，使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。

相对熵=交叉熵-信息熵：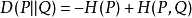

示例假如一个字符发射器，随机发出0和1两种字符，真实发出概率分布为A，但实际不知道A的具体分布。通过观察，得到概率分布B与C，各个分布的具体情况如下：

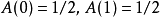
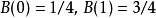
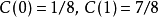可以计算出得到如下：

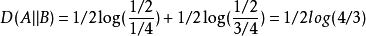
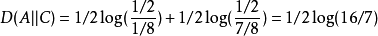
也可以看出，按照概率分布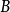进行编码，要比按照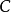进行编码，平均每个符号增加的比特数目少。从分布上也可以看出，实际上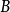要比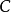更接近实际分布（因为其与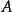分布的相对熵更小）

应用相对熵可以衡量两个随机分布之间的距离，当两个随机分布相同时，它们的相对熵为零，当两个随机分布的差别增大时，它们的相对熵也会增大。所以相对熵（KL散度）可以用于比较文本的相似度，先统计出词的频率，然后计算相对熵。另外，在多指标系统评估中，指标权重分配2是一个重点和难点，也通过相对熵可以处理。