[科普中国]-稳定极限环

简介

在数学中，特别是在动态系统理论里，一个二维平面或二维流形上的极限环是相空间里的一个闭合的轨迹，使得至少另一个轨迹会随自变量变化而逐渐逼近它（在自变量趋于正无穷或负无穷的时候）。

如果当自变量（或者说时间）：t趋于正无穷时，所有的邻近轨迹都趋近于极限环，那么所在的流形被称为稳定的，或者称极限环是稳定的（吸引的）。反之，如果t趋于负无穷时，所有的邻近轨迹都趋近于极限环，那么称流形是不稳定的或者极限环是不稳定的（非吸引的）。在所有其它情况下，流形既不是稳定也不是不稳定的。

稳定的极限环会导致持续振荡的情况：若一开始轨迹是极限环，则关于轨迹的任意的小扰动都会导致系统重新回到极限环的状态。1

基本概念定义1：

对于平面自治系统(1)：

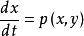
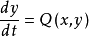
有闭轨线Γ，若存在δ>0使系统(1)在Γ的两侧邻域S(Γ，δ)内的一切轨线均以Γ为其Ω或A极限集，则称Γ为系统(1)的一个极限环。

容易看出，这样定义的极限环实际上就是一条孤立的闭轨线。

定义2：

若系统(1)在其极限环Γ外侧(内侧)足够小邻域内的轨线均以Γ为Ω极限集，则称Γ为外(内)稳定极限环；

若均以Γ为A极限环，则称Γ为外(内)不稳定环；

若Γ既外稳定(不稳定)又内稳定(不稳定)，则称Γ为稳定(不稳定)极限环；

若Γ的一侧稳定另一侧不稳定，则称Γ为半稳定极限环。

定义3：

对于系统( 1) 而言，均设

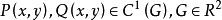
设函数 F( x, y) ∈C1(G)，易知曲线族 F( x, y) =C 与轨线相切点的轨迹方程是：

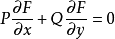
我们称曲线( 2) 为系统( 1) 的切性曲线。同时，注意到 F( x,y) 沿系统( 1) 的轨线关于 t 的全导数为：

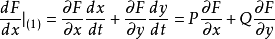
判断极限环的稳定性的方法（1）一种是根据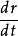 的符号结合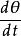 的表达式

（2）如果沿着系统的极限环Γ有

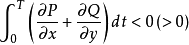
则Γ是稳定(不稳定)的，其中T是Γ的周期。

举例考察系统

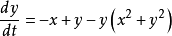
在全平面极限环的存在性及稳定性。

取曲线族：

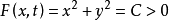
求得：

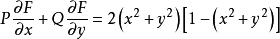
所以该系统的切性曲线对应于原点O和单位圆周x2+y2=1。在单位圆周内，除点O外不含切性曲线上的点，由定理知，单位圆内系统不存在闭轨;同样单位圆外系统也不存在闭轨。容易验证，单位圆周是系统的轨线，并且它是唯一稳定的极限环。2