定义
对一序列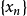 ,令
,令
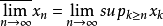
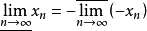
(二者必定存在,且 )分别称为当n→∞时,x?的上极限与下极限。关于其他极限过程的上、下极限可类似定义。1
)分别称为当n→∞时,x?的上极限与下极限。关于其他极限过程的上、下极限可类似定义。1
数列上极限给定无穷数列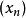 ,它的一切收敛子数列的极限值的上确界值,称为该无穷序列的上极限。
,它的一切收敛子数列的极限值的上确界值,称为该无穷序列的上极限。
或定义为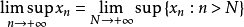 。因为
。因为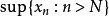 是递减的,所以讨论其极限值是有意义的。
是递减的,所以讨论其极限值是有意义的。
集合上极限给定无穷集合列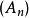 ,
,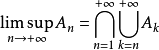 称为无穷集合列的上极限集,含义为属于无穷个
称为无穷集合列的上极限集,含义为属于无穷个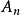 的元素组成的集合。2
的元素组成的集合。2
运算性质在同一极限过程中下列式子成立:
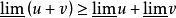

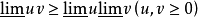
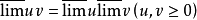
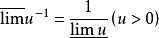 若u存在,则上面的不等式成为等式。
若u存在,则上面的不等式成为等式。
比较性质若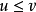 ,则
,则
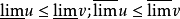 若
若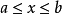 ,a,b是常数,则
,a,b是常数,则
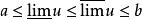
与极限的关系lim u存在,则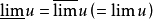
lim u=l,则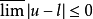




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国