[科普中国]-多值函数

概述

多值函数定义：设X是一个非空数集，Y是非空数集 ，f是个对应法则 ， 若在X中有至少一个元素x，按对应法则f，Y有至少两个元素y与之对应，且对X中的所有元素x，按对应法则f，都有Y中的元素y与之对应，则称f为从X到Y的多值函数，记作y=f(x)。1

若对定义域每一个自变量x，其对应的函数值f(x)是唯一的，则称f(x)是单值函数，反之则称f(x)是多值函数。关键词“每一个”，“唯一的”。

单值函数定义：设X是一个非空数集，Y是非空数集 ，f是个对应法则 ， 若对X中的每个x，按对应法则f，使Y中存在唯一的一个元素y与之对应 ， 就称对应法则f是X上的一个函数，记作y=f(x)。习惯上也说y是x的函数。

这两个定义的区别可抓关键词的变化，“唯一的”变为“至少一个”且具备“一对多”的情况。

举例多值函数的例子：

（1）若│f(x)│=2x-1，则f(x)=±(2x-1)，一个自变量x对应两个函数值。

（2）y=sinx (x∈R)在R上的反函数（注：在单值函数里，是"在[-π/2,π/2]上为多值函数）

（3）y=Arcsinx，一个自变量x对应无数个函数值。

（4）每个大于0的实数都有二个实数的平方根，例如4的平方根是{−2, +2}.，0的平方根是0。

（5）一般而言，许多不为0的复数都有二个平方根、三个立方根、n个n次方根，只有0的n次方根为0。

（6）复对数函数是多值函数。log(a+bi)（ a和b为实数）的值是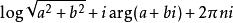，其中 n为任意整数。 .

（7）反三角函数为周期性的多值函数，例如

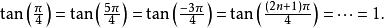
因此，arctan(1)在本质上会对应许多数值：π/4, 5π/4, −3π/4等。若限制其tanx的定义域在−π/2