主要思想
数学上,分离变量法是一种解析常微分方程或偏微分方程的方法。使用这方法,可以借代数来将方程式重新编排,让方程式的一部分只含有一个变量,而剩余部分则跟此变量无关。这样,隔离出的两个部分的值,都分别等于常数,而两个部分的值的代数和等于零。1
利用高数知识、级数求解知识,以及其他巧妙的方法,求出各个方程的通解。最后将这些通解“组装起来”。分离变量法是求解波动方程初边值问题的一种常用方法。
常微分方程第一种方法假若,一个常微分方程可以写为2
 。
。
设定变量 y=f(x)。那么,
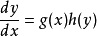 .(1)
.(1)
只要是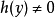 ,就可以将方程式两边都除以h(y) ,再都乘以 dx :
,就可以将方程式两边都除以h(y) ,再都乘以 dx :
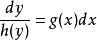 。
。
这样,可以将两个变量x ,y 分离到方程式的两边。由于任何一边的表达式跟另外一边的变量无关,表达式恒等于常数k 。因此,可以得到两个较易解的常微分方程;
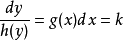 。
。
第二种方法有些不喜欢用莱布尼茨标记(Leibniz's notation) 的数学家,或许会选择将公式 (1) 写为
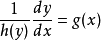 。
。
这写法有一个问题:无法比较明显的解释,为什么这方法叫作分离变量法?
随着 x积分公式的两边,可以得到
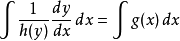 。(2)
。(2)
应用换元积分法,
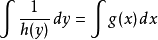 。
。
假如,可以求算这两个积分,则这常微分方程有解。这方法允许将导数 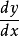 当做可分的分式看待,可以较方便的解析可分的常微分方程。
当做可分的分式看待,可以较方便的解析可分的常微分方程。
偏微分方程给予一个n 元函数 的偏微分方程,有时候,为了将问题的偏微分方程式改变为一组常微分方程,可以猜想一个解答;解答的形式为2
的偏微分方程,有时候,为了将问题的偏微分方程式改变为一组常微分方程,可以猜想一个解答;解答的形式为2
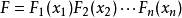 ,
,
或者
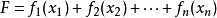 。
。
时常,对于每一个自变量 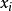 ,都会伴随着一个分离常数。如果,这个方法成功,则称这偏微分方程为可分偏微分方程(separable partial differential equation)。
,都会伴随着一个分离常数。如果,这个方法成功,则称这偏微分方程为可分偏微分方程(separable partial differential equation)。
例子设复数 ,两边对
,两边对 求导数,得
求导数,得
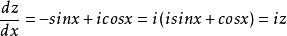
分离变量,得
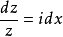
对两边积分,得

即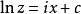
取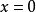 得,
得,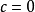 ,故有
,故有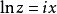 ,即
,即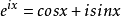




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国