[科普中国]-平稳过程

简介

平稳过程：统计特性不随时间的推移而变化的随机过程1。

例如，一台稳定工作的纺纱机纺出的纱的直径大小，受各种随机因素影响，在某一标准值周围波动，在任意若干时刻处，直径之间的统计依赖关系，仅与这些时刻之间的相对位置有关，而与其绝对位置无关，因而直径的变化过程可以看作一个平稳过程。具有近似于这种性质的随机过程，在实际中是大量存在的。

在数学中，平稳过程（Stationary process）或者严格平稳过程（Strictly-sense stationary,SSS）是在固定时间和位置的概率分布与所有时间和位置的概率分布相同的随机过程1。因此，数学期望和方差这些参数也不随时间和位置变化。

例如，白噪声（AWGN）就是平稳过程，铙钹的敲击声是非平稳的。尽管铙钹的敲击声基本上是白噪声，但是这个噪声随着时间变化：在敲击前是安静的，在敲击后声音逐渐减弱。

在时间序列分析中稳态作为一个工具使用，在这里原始数据经常转换为平稳态，例如经济学数据经常随着季节或者价格水平变化。如果这些过程是平稳过程与一个或者多个呈现一定趋势的过程的线性组合，那么这些过程就可以表述为趋势平稳。将这些数据进行转换保留平稳数据用于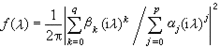分析的过程称为解趋势（de-trending）。

采样空间也是离散的离散时间平稳过程称为Bernoulli scheme，离散采样空间中每个随机变量可能取得 N'个可能值中的任意一个。当 N = 2 的时候，这个过程叫做伯努利过程。

概念1）定义

设{X(t），t∈T}是一随机过程，如果对于任意的n≧1和任意的t1,t2....,tn∈T以及使t1+τ，t2+τ，...,tn+τ∈T的任意实数τ，n维随机变量（X(t1），X(t2），...，X(tn））和（X(t1+τ），X(t2+τ），...,X(tn+τ））有相同的联合分布函数，即

F(t1,t2,...,tn;x1,x2,...xn)=F(t1+τ，t2+τ，...,tn+τ;x1,x2,...,xn)

ti∈T，τ∈R,i=1,2,...,n

则称{X(t),t∈T}是严平稳过程（强平稳过程或狭义平稳过程），或称{X(t),t∈T}具有严平稳性2。

2）主要性质和结论

⑴严平稳过程的所有一维分布函数F(t;x)=F(x）与t无关；二维分布函数仅是时间间隔的函数，而与两个时刻本身取值无关，即

F(t1,t2;x1,x2）=F(t1+τ，t2+τ；x1,x2）=F(0,t2-t1;x1,x2）

⑵若{X(t），t∈T}是正态过程，则{X(t），t∈T}是严平稳过程的充要条件是{X(t），t∈T}位宽平稳过程。

理论发展平稳过程理论在无线电技术和自动控制等领域有着广泛的应用，并且是诸如时间序列分析、信号分析、滤波、预测理论以及控制理论等应用学科的重要工具。

相关举例设X=(X(t),t∈T）是一个取复数值的随机过程，其中指标集T为整数或实数全体（分别称为离散指标和连续指标）。如果对任意的自然数n及任意的t1，t2，…tn， 的概率分布与（X(t1），X(t2），...，X(tn））的概率分布相同，则称X为严平稳过程1。如果二阶绝对矩，而且对任意的t，τ∈T，均值（见数学期望）EX(t），m（常数），协方差（与τ无关），则称X为宽平稳过程。Г（t）称为X 的协方差函数。一个严平稳过程，如果它的二阶矩有穷，则一定也是宽平稳的（见矩）。

宽平稳过程概述给定二阶矩过程{X(t),t∈T}，如果对任意的t,t+h∈T,有

（1）E[X(t)]=Cx（常数） （2）E[X(t)X(t+h)]=R(h)

则称{X(t),t∈T}为宽平稳（随机）过程或广义平稳（随机）过程。

注：

二阶矩过程定义：如果随机过程{X(t),t∈T}对每一个t∈T，二阶矩E[X(t)·X(t)]都存在，那么称它为二阶矩过程。

要证明某个随机过程是否是宽平稳过程（广义平稳过程）就必须的满足以上定义中的三个条件：

（1）E[X(t)]=Cx（常数） ；

（2）E[X(t)X(t+h)]=R(h) ；

（3）E[X2(t)严平稳随机过程与宽平稳随机过程区别联系

（1）一个宽平稳过程不一定是严平稳过程，一个严平稳过程也不一定宽平稳过程。

例1、X(n)=sinwn，n=0,1,2，…，其中w服从U（0,2π）,随机过程{X(n),n=0,1,2，…}是宽平稳过程，但不是严平稳过程。

例2、服从柯西分布的随机变量序列是严平稳随机过程，但不是宽平稳随机过程。

（2）宽平稳过程定只涉及与一维、二维分布有关的数字特征，所以一个严平稳过程只要二阶矩存在，则必定是宽平稳过程。但反过来，一般是不成立的。

（3）正态过程是一个重要特例，一个宽平稳的正态过程必定是严平稳的。这是因为：正态过程的概率密度是由均值函数和自相关函数完全确定的，因而如果均值函数和自相关函数不随时间的推移而变化，则概率密度函数也不随时间的推移发生变化。

宽平稳过程的线性预测这是由Α.Η.柯尔莫哥洛夫和N.维纳在1940年左右提出并解决的问题。对于一个均值为0的宽平稳过程X=(X(t），t∈T），随机变量集{X(s），β∈T，s≤t}表示到时刻t为止所能观测到的过程的历史，用Mt(X）表示由这些随机变量的一切有限线性组合及其均方极限所构成的希尔伯特空间。

设τ>0，所谓"τ步"线性预测，就是要用Mt(X）中的随机变量来估计还未曾观测的X(t+τ)(t+τ∈T）；而线性最优预测，就是要在Mt(X）中选择（t，τ），使预测误差的方差达到最小。可以证明（t，τ）唯一存在，它就是X(t+τ）在空间上的投影。如果对任意的t，β∈T，都有=Ms(X），则称过程为决定的或奇异的，这时，即可以无差误地进行预测；如果所有Mt(X）的公共部分仅包含零，则称过程为纯非决定的或正则的。一般的宽平稳过程 X可以分解成相互正交的两部分之和：其中Xr是纯非决定的宽平稳过程，Xs是决的宽平稳过程。这时，Xr可以按离散指标或连续指标而分别表示为一个正交随机序列（ξ（t),t∈T）的向后的滑动和或一个正交增量过程 （ξ（t），t∈T) 的向后的滑动积分（对正交增量过程的积分）。宽平稳过程的这一分解称为沃尔德分解。

此外，宽平稳过程X本身为纯非决定的充分必要条件是，它有谱密度ƒ（λ），具有有理谱密度的过程是纯非决定过程的重要特例。

多维宽平稳过程设X(t)=(X1(t),X2(t），…，Xk(t））┡是由k个分量组成的，而且均值EX(t）为常值向量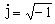，协方差阵E(X(t+τ）-m)(X（τ）-m)*=Г（t）与τ无关，则称X=(X(t),t∈T）为k维宽平稳过程，其中记号“┡”与“*”分别表示向量或矩阵的转置与共轭转置2。这时，Г（t）与X(t）在形式上有和一维情形一样的谱分解，只是 F（λ）（或ƒ（λ））变为k×k的函数矩阵，它的对角线元就是各分量本身的谱分布（或密度）函数，而它的非对角线元称为相应分量的互谱分布（或密度）函数，而且ƒ（λ）=ƒ*（λ）是非负定矩阵。关于多维宽平稳过程的线性预测问题，也有类似于一维的结果。

齐次随机场如果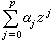随机过程X=(X(t），t∈T）的指标集T是k维整值向量或实值向量的全体，且其均值与协方差函数满足与宽平稳过程的定义相同的条件，则称X为齐次随机场或k指标平稳过程。这时X(t）与Г（t）也有相应的谱分解。如果进一步，Г（t）只与指标向量t的长度（tj为t的分量）有关，则称X为迷向场。齐次场在力学的湍流理论中很有用。齐次场的线性预测问题比宽平稳过程的情形要复杂得多，中国学者江泽培开始了这方面的工作。

相关介绍严平稳过程的遍历定理

遍历定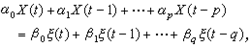理 关于严平稳过程，最重要的性质是以概率1成立的遍历定理，或称为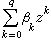各态历经定理3。这一名词来自物理学。任何严平稳过程X=(X(t），t∈T）都可看作是由某个概率空间 (,F,P）上的保测变换群{St，t∈T}作用于随机变量X(0）而产生的，其中对任意的，实数x及随机变量ξ，满足条件，而X(t)=StX(0）。用表示使StA=A对任何t∈T成立的事件A的全体，则是F的子σ域。如果均值EX(0）存在，则以概率1收敛于条件期望E{X(0)|}。如果中只含概率为1或为0的事件，则称过程X为遍历的，这时以概率1收敛于EX(0)=EX(t）。后一结果也称为严平稳过程的强大数律，它表明，过程几乎所有的样本对时间的平均都趋近于每一时刻的过程值对概率分布的平均。