[科普中国]-负二项分布

简介

满足以下条件的称为负二项分布

1. 实验包含一系列独立的实验。

2. 每个实验都有成功、失败两种结果。

3. 成功的概率是恒定的。

4. 实验持续到r次成功，r可以为任意正数。1

当r是整数时，负二项分布又称帕斯卡分布（巴斯卡分布），其概率质量函数为（其中一种形式，两种形式对比看下文）：

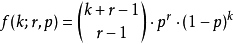它表示，已知一个事件在伯努利试验中每次的出现概率是p，在一连串伯努利试验中，一件事件刚好在第r + k次试验出现第r次的概率。

定义假设有一组独立的伯努利数列，每次实验有两种结果“成功”和“失败”。每次实验的成功概率是p，失败的概率是1－p。我们得到一组数列，直到预定的成功次数发生r次。那么结果为“成功”的随机数X会服从负二项分布（或帕斯卡）分布：

X~NB(r;P)

我们在现实生活中也常有应用，成功和失败的结果可能或者可能不是我们平时所认认为的“好”与“坏”。假设我们把负二项分布用在一台设备在故障前正常运行的天数的模型，这种情况下，设备一天运行正常，记为结果“成功”，反之故障的话结果为“失败”。如果我们把负二项分析用在动作员尝试射门得分前的尝试次数模型，这种情况下，每次不成功的尝试在模型里为“成功”，并且得分记为“失败”。如果我们抛硬币，负二项分布可以把头像一面作为“成功”来记数，在我们提到失败的结果之前。在下面的概率密度函数里，P是成功的概率，1－p是失败的概率。2

负二项分布的概率密度函数为：

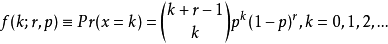
这里的括号里的数为二项分布的系数，并且等于

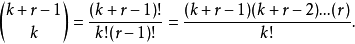
该数可以按下面的格式表示，也正是解释了“负二项”的名字的由来：

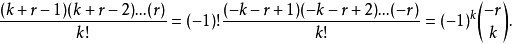
为了理解上面的概率密度函数，因为k+r次重复试验的结果假设是独立的，需要注意每个特定的k作为成功和r失败的数列为(1-p)p。因为第r个失败是最后发生的，所以需要k+r-1次重复实验中有k次成功的。上面的二项分布系数，正好它的组合长度为k+r-1。3

递推公式为

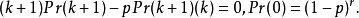
举例举例说，若我们掷骰子，掷到一即视为成功。则每次掷骰的成功率是1/6。要掷出三次一，所需的掷骰次数属于集合 { 3, 4, 5, 6, ... } 。掷到三次一的掷骰次数是负二项分布的随机变量。要在第三次掷骰时，掷到第三次一，则之前两次都要掷到一，其概率为(1 / 6)。注意掷骰是伯努利试验，之前的结果不影响随后的结果，即每次实验为独立随机实验。若要在第四次掷骰时，掷到第三次一，则之前三次之中要有刚好两次掷到一，在三次掷骰中掷到2次1的概率为：

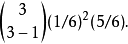
第四次掷骰要掷到一，所以要将前面的概率再乘(1/6)。

期望：参数为(r, p)的负二项分布的数列k+r的期望是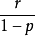。为了更直观的观察，想象上面的实验进行了许多次，也就是说，进行特定的实验直到r个失败出现，然后另外的一个特定的实验，然后是另外的实验，等等。写下每次实验的这些尝试的次数：a, b, c…并且把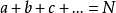。现在我们对失败的预期为N(1-p)。我们说实验重复了n次，并且总共有有nr个失败。所以我们估计nr=N(1-p)，所以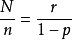。注意N/n仅仅是平均每个实验的尝试次数。这就是我们所说的“期望”。每次实验的平均成功的尝试次数为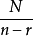，期望值等于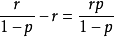。3

实数r的延伸把负二项分布的定义延伸到到的参数r。尽管很难想象一个非整数的失败次数，我们仍然可以通过概率密度函数在形式上定义这个分布。

就像之前，我们说X服从负二项分布（或者波利亚分布），如果它有一个如下所示的概率密度函数：

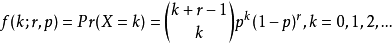
这里r是一个正实数。通过乘法公式，二项分布系数可以重新定义，并且可以重新写成gamma分布的公式。

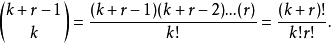
注意二项分布序列和上面的内容里，0≤p≤1.

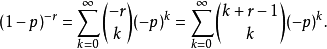
因此，概率密度函数的项实际上可以合并成一项。

替代公式有一些书里的负二项分布的公式定义可能和这里的有一些小区别。最常见的变化就是：

X是实验总次数，得到r个失败的尝试。不仅仅是成功的次数。因此，实验总次数等于失败数加成功数，这个不同于这里定义的X。3

为了把公式换这种定义进行转换，把k用k-r代替，并且从均值、中位数，或者众数中减去r。为了将按本节定义的负二项分布的公式转换成本文里的公式，需要用k+r代替k，并且在均值，中位数，众数中加上r。

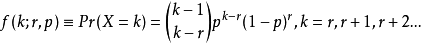
这个可能比上面的版本看起来更像二项分布，注意二项分布的参数是按顺序减少的：最后一个失败必然在最后发生，所以其它的事件有更少的可利用的位置，在计算顺序可能性时。

注意这里的负二项分布的定义没有推广到正实数r。

P表示失败的概率，不是成功的。为了把公式进行转换，每个地方用1-p代替p。X定义为失败次数，而不是成功的，这里的定义X为失败的，但P是成功的，和前面X表示成功但P表示失败概率的情况用同样的公式。但是失败和成功的描述是一致的，并且和前面的进行替换。

这两个替代公式可能会同时使用，比如X表示总次数，P表示失败次数。

负二项回归，分布是在均值m项里就定义了，并且和线性回归或者其它的一般线性回归的解释变量相关。概率密度函数变为

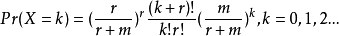
方差可以写成m+m/r，参数r参考离散参数，形状参数，集中系数，或者非均匀或者集中参数。集中参数特别常用于生态学用来描述独立微生物。减少聚集参数r到0，与增加微生物聚集相一致。0到正无穷的增加相当于没有聚合，可以被描述成泊松分布。一些负二项回归使用r的倒数并且当作分散度参数。1

有时候分布使用均值u和方差σ来参数化分布，这种情况下：

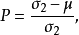
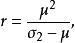
事件在r为整数的特定情况下，负二项分布也可以称作帕斯卡分布。它是在独立重复的伯努利实验中成功和失败的数目的概率分布。因为k+r次概率为p的成功的伯努利实验可以得到最后一次为失败的k次成功和r次失败的概率。换句话说，负二项分布为成功概率为p的伯努利过程中第r次失败前的成功次数的概率分布。一个伯努利过程是离散的过程。因此，实验次数，失败、成功次数都是整数。1