概述
玻尔兹曼(L.E.Boltzmann)将麦克斯韦分布律推广到有外力场作用的情况。在等宽的区间内,若E1>E2,则能量大的粒子数dN1小于能量小的粒子数dN2,状态即粒子优先占据能量小的,这是玻尔兹曼分布律的一个重要结果。
经过将近一个世纪的传播,物理学界、化学界渐渐接受了道尔顿的“原子—分子模型”,但原子、分子的确凿证据迟迟没有找到。恰恰此时,一股更强大的科学成就——热力学第一、第二定律出现了。热力学原则上解决了一切化学平衡的问题。1892年,物理化学家奥斯特瓦尔德试图在此基础上证明,将物理学和化学问题还原为原子或分子之间的力学关系是多余的。他试图将“能量”赋以实物一样的地位,甚至要把物质还原为能量。他提出“世界上的一切现象仅仅是由于处于空间和时间中的能量变化构成的”。1
在统计学中,麦克斯韦- 玻尔兹曼分布是一种特殊的概率分布,以詹姆斯·克拉克·麦克斯韦和路德维希·玻尔兹曼的名字命名。它一开始在物理中定义并使用是为了描述(特别是统计力学中描述理想气体)在理想气体中粒子自由移动的在一个固定容器内与其它粒子无相互作用的粒子速度,除了它们相互或与它们的热环境交换能量与动量所产生的非常短暂的碰撞。在这种情况下粒子指的是气态粒子(原子或分子),并且粒子系统被假定达到热力学平衡。2在这种分布最初从麦斯威尔1960年的启发性的基础上衍生出来时34,玻尔兹曼之后对这种分布的物理起源进行了大量重要调查。

粒子速度概率分布指出哪一种速度更具有可能性:粒子将具有从分布中随机选择的速度,并且比其它选择方法更可能在速度范围内。 分布取决于系统的温度和粒子的质量。5 麦克斯韦 - 波尔兹曼分布适用于经典理想气体,这是一种理想化的实际气体。 在实际气体中,存在可以使其速度分布与麦克斯韦 - 波尔兹曼形式不同的各种效应(例如,范德华相互作用,涡流,相对论速度限制和量子交换相互作用)。 然而,常温下的稀释气体表现得非常接近于理想的气体,麦克斯韦速度分布对于这种气体是非常好的近似值。 因此,它形成了动力学气体理论的基础,其提供了许多基本气体性质(包括压力和扩散)的简化解释。6
麦斯威尔- 玻尔兹曼分布函数麦斯威尔- 玻尔兹曼分布函数是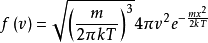 。
。
在方程中,m是粒子质量,kT是玻尔兹曼常数与热力学温度的乘积。要注意有趣的一点是,麦克斯韦 - 波尔兹曼分布不会随着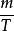 值即分子质量与其绝对温度的比值而变化;数学表达式是(f(v)的导数/(m /T)的导数)= 0。该概率密度函数给出了以
值即分子质量与其绝对温度的比值而变化;数学表达式是(f(v)的导数/(m /T)的导数)= 0。该概率密度函数给出了以 附近速度求出粒子的每单位速度的概率,该方程式简单地是具有分布参数
附近速度求出粒子的每单位速度的概率,该方程式简单地是具有分布参数 的麦克斯韦分布。 在概率理论中,麦克斯韦-波尔兹曼分布是具有三个自由度和尺度参数
的麦克斯韦分布。 在概率理论中,麦克斯韦-波尔兹曼分布是具有三个自由度和尺度参数 的奇偶分布。由分布满足的最简单的常微分方程为:
的奇偶分布。由分布满足的最简单的常微分方程为: ,
,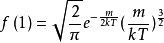 。
。
请注意,分布(函数)与概率不同。 分布(函数)代表平均数,如所有三种统计数据(Maxwell-Boltzmann,Bose-Einstein,Fermi-Dirac)。 使用达尔文 - 福勒方法的平均值,得到麦克斯韦-玻尔兹曼分布作为精确结果。
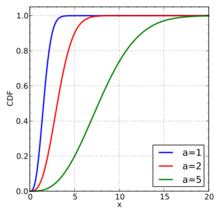
求典型速度平均速度,最可能的速度(众数)和均方根可以从麦克斯韦分布的性质获得。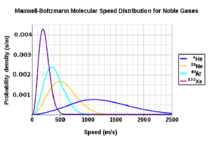
最可能的速度vp是系统中任何分子(质量同等于m)最有可能拥有的速度,并且对应于f(v)的最大值或模式。 要找到它,我们需要计算导数df/dv,将其设为零并求解v:
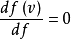 。
。
通过此式得出:
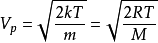 ,
,
其中R是气体常数,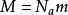 是物质的摩尔质量。对于室温(300K)中的氮气,已知
是物质的摩尔质量。对于室温(300K)中的氮气,已知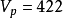 ,平均速度是速度分布的预期值:
,平均速度是速度分布的预期值:
 。
。
均方根速度是二阶转速:
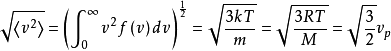 。
。
典型速度关系如下:
 ;
;
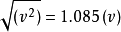 ;
;
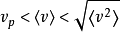 ;
;
推导与联系詹姆斯·克莱斯·麦斯威尔(James Clerk Maxwell)1860年的原始推导是基于气动动力学理论的分子碰撞以及速度分布函数中的某些对称性的论证;麦克斯韦还提出了一个早期的论据,认为这些分子碰撞需要平衡的趋势。734在麦克斯韦尔(Maxwell)之后,路德维希·波兹曼(Ludwig Boltzmann)也在1872年得出了机械理论的分布,并认为由于碰撞气体应该随着时间的推移趋向于这种分布。 他后来(1877年)在统计热力学的框架下再次导出了此分布。 本节的推导是按照玻尔兹曼1877的派生方式,从称为麦斯威尔- 玻尔兹曼统计(从统计热力学)的结果开始。 麦斯威尔- 玻尔兹曼统计量给出了在某些假设条件下给定单粒子微观状态中发现的平均粒子数:28
⑴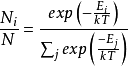
在上式中:
i和j是单粒子微态的指标(或标签)
Ni是单粒子微观状态i中的平均粒子数,
N是系统中的粒子总数,
Ei是microstate i的能量,
T是系统的平衡温度,
k是波尔兹曼常数。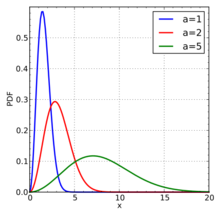
这个方程的假设是粒子不相互作用,而且它们是典型的; 这意味着每个粒子的状态可以独立于其他粒子的状态来考虑。 另外,假定颗粒处于热平衡状态。 方程式⑴中的分母只是一个归一化因子,因此Ni / N加起来为1,换句话说,它是一种分区函数(对于单粒子系统,不是整个系统的通常分区函数)。
由于速度和速度与能量有关,方程⑴可用于推导出气体颗粒的温度和速度之间的关系。 所需要的是发现能量中微观状态的密度,这是通过将动量空间分成相等大小的区域来确定的。
动量矢量的分布势能被认为是零,所以所有能量都是动能的形式。 大量非相对论粒子的动能与动量之间的关系是:
⑵ ,其中P方是动量矢量P= [Px,Py,Pz]的平方。 因此,我们可以将等式(1)改写为:⑶
,其中P方是动量矢量P= [Px,Py,Pz]的平方。 因此,我们可以将等式(1)改写为:⑶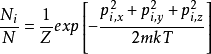 ,⑶中Z是分配函数,对应于等式⑴中的分母。 这里m是气体的分子质量,T是热力学温度,k是玻尔兹曼常数。 Ni / N的这种分布与用于找到具有这些动量分量值的分子的概率密度函数
,⑶中Z是分配函数,对应于等式⑴中的分母。 这里m是气体的分子质量,T是热力学温度,k是玻尔兹曼常数。 Ni / N的这种分布与用于找到具有这些动量分量值的分子的概率密度函数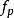 成比例,因此:⑷
成比例,因此:⑷ 。归一化常数c可以通过“具有一定动量的分子的概率必须为1”来确定。因此,方程⑷上的px,py和pz所有的积分必须为1。可表达为:⑸
。归一化常数c可以通过“具有一定动量的分子的概率必须为1”来确定。因此,方程⑷上的px,py和pz所有的积分必须为1。可表达为:⑸ 。将等式⑸代入等式⑷得出:⑹
。将等式⑸代入等式⑷得出:⑹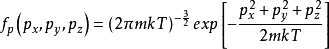 。
。
该分布被认为是三个独立的正态分布变量 ,
,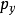 和
和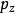 的乘积,方差为
的乘积,方差为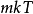 。此外,可以看出,动量的大小将以麦斯威尔- 玻尔兹曼分布分布,其中
。此外,可以看出,动量的大小将以麦斯威尔- 玻尔兹曼分布分布,其中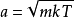 。在气体框架的动力学理论中,可以使用H平衡的H定理更基本地获得麦克斯韦 - 波尔兹曼分布的动量(或等同于速度)。
。在气体框架的动力学理论中,可以使用H平衡的H定理更基本地获得麦克斯韦 - 波尔兹曼分布的动量(或等同于速度)。
能量的分布能量分布是强大的:⑺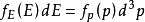 ,
, 。其中
。其中 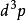 是对应于能量间隔dE的动量的无穷小相空间体积。 利用能量 - 动量弥散关系的球面对称性,可用
是对应于能量间隔dE的动量的无穷小相空间体积。 利用能量 - 动量弥散关系的球面对称性,可用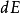 表示为:⑻
表示为:⑻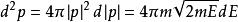 。将⑻带入⑺中,并且使用E(能量)表达一切,我们得到如下等式:
。将⑻带入⑺中,并且使用E(能量)表达一切,我们得到如下等式:
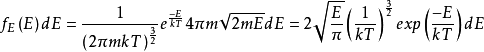 ,最终得到:
,最终得到:
⑼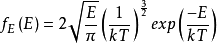 。
。
由于能量与三个正态分布的动量分量的平方和成正比,所以该分布是伽马分布; 特别是它是一个具有三个自由度的卡方分布。通过均分定理,这种能量在所有三个自由度中均匀分布,使得每个自由度的能量作为具有一个自由度的卡方分布而分布: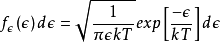 。
。
在上式中ε是每自由度的能量。 在平衡状态下,这种分布将适用于任何数量的自由度。 例如,如果某一种粒子是具有固定偶极矩的刚性质量偶极子,则它们将具有三个平移自由度和另外两个旋转自由度。 每个自由度的能量将根据上述具有一个自由度的卡方分布来描述,并且总能量将根据具有五个自由度的卡方分布来分布。 这对气体比热容理论有影响。
麦克斯韦-玻尔兹曼分布也可以通过考虑气体作为近似ε>> k T的量子气体来获得。9
速度矢量的分布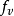 通过下式确认速度 概率密度与动量概率密度函数成比例:
通过下式确认速度 概率密度与动量概率密度函数成比例: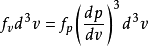 。
。
通过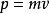 得到:
得到: 。
。
上式是麦克斯韦-波尔兹曼速度分布。 关于在无穷小因子中找到具有速度的粒子的概率是: 。像动量一样,这种分布被认为是三个独立的正态分布变量
。像动量一样,这种分布被认为是三个独立的正态分布变量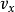 ,
, ,
, ,但是方差是
,但是方差是 。还可以看出,矢量速度
。还可以看出,矢量速度 的麦克斯韦-玻尔兹曼速度分布是三个方向中的每一个分布的产物:
的麦克斯韦-玻尔兹曼速度分布是三个方向中的每一个分布的产物: 。其中对于单个方向上的分布是:
。其中对于单个方向上的分布是: 。
。
速度矢量的每个分量具有平均值为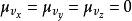 和标准差为
和标准差为 的正态分布,因此向量具有三维正态分布,是一种特定类型的多变量正态分布,平均值为
的正态分布,因此向量具有三维正态分布,是一种特定类型的多变量正态分布,平均值为 ,标准差为
,标准差为 。
。
速度的麦斯威尔- 玻尔兹曼分布可以立即从速度矢量的分布得到。 注意速度是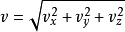 ,并且体积单位为球面坐标
,并且体积单位为球面坐标 ,其中φ和θ是速度矢量的“路线”(方位角)和“路径角”(速度矢量的仰角)。 将速度的普遍概率密度函数的路线(从0到2π)和路径角(从0到π),以速度代入矢量分量的平方和之和,得到速度分布。10
,其中φ和θ是速度矢量的“路线”(方位角)和“路径角”(速度矢量的仰角)。 将速度的普遍概率密度函数的路线(从0到2π)和路径角(从0到π),以速度代入矢量分量的平方和之和,得到速度分布。10




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国