[科普中国]-共轭梯度法

简介

共轭梯度法最早是由Hestenes和Stiefle提出来的，在这个基础上，Fletcher和Reeves （1964）1首先提出了解非线性最优化问题的共轭梯度法。由于共轭梯度法不需要矩阵存储，且有较快的收敛速度和二次终止性等优点，现在共轭梯度法已经广泛地应用于实际问题中。

共轭梯度法是一个典型的共轭方向法，它的每一个搜索方向是互相共轭的，而这些搜索方向d仅仅是负梯度方向与上一次迭代的搜索方向的组合，因此，存储量少，计算方便。

方法的表述简述设我们要求解下列线性系统2

，

其中n-×-n矩阵A是对称的（也即AT=A），正定的（也即xTAx> 0对于所有非0向量x属于R），并且是实系数的。

将系统的唯一解记作x*。

最后算法经过一些简化，可以得到下列求解Ax=b的算法，其中A是实对称正定矩阵。

x0= 0

k= 0

r0=b-Ax

直到rk足够小：

k=k+1

ifk = 1

p1=r0

else

end if

其中xk=xk-1+ αkpk，rk=rk-1- αkApk。

end repeat

结果为xk。

作为直接法我们说两个非零向量u和v是共轭的（相对于A），如果

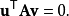
由于A是对称和正定的，所以左侧定义了内积：

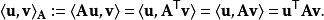当且仅当它们相对于该内积正交时，两个向量是共轭的。 共轭是一个对称关系：如果u与v共轭，则v与u共轭。 假设

是一组n维共轭向量。那么P 组成了 的基，在此基础上我们表述 解x∗为：

基于这个扩展，我们计算：

其中：

这给出了求解方程的以下方法：Ax = b：找到n个共轭方向的序列，然后计算系数αk。

作为迭代法如果我们仔细选择共轭向量pk，那么我们可能不需要所有这些来获得解x*的好的近似值。 因此，我们将共轭梯度法视为迭代法。这也使我们能够大致解决n大到非常大的系统，因为直接方法花费太多时间。

我们假设x0是x∗的初始值，我们可以不失一般性的假设x0=0(否则，考虑用系统Az=b−Ax0代替)。

我们从x0开始搜索解决方案，在每次迭代中，我们需要一个指标来告诉我们我们是否更接近解决方案x*（这对我们来说是未知的）。

该度量来自于以下事实：解x *也是以下二次函数的唯一最小值：

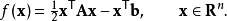
这表明在x = x0处采用第一基矢量p0为f的梯度的负值。 f的梯度等于Ax-b。 从“猜测的解决方案”x0开始（如果我们没有理由猜测其他任何东西，我们总是猜测x0 = 0），这意味着我们取p0 = b - Ax0。

在此基础上的其他向量将与梯度共轭，因此称为共轭梯度法。

让rk成为第k步的残差：

注意，rk是x = xk处的f的负梯度，因此梯度下降法将是沿rk方向移动。 在这里，我们坚持方向pk彼此共轭。 我们还要求下一个搜索方向由当前的残差和所有先前的搜索方向构成，这在实践中是足够合理的。

共轭约束是一种正交类型约束，因此该算法与Gram-Schmidt正交归一化相似。

给出以下表达式：

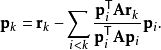
按照这个方向，下一个最佳位置由下式给出：

其中

由于pk和xk是共轭的，所以最后一个等式成立。

例子考虑线性系统Ax = b由下式给出

我们将从初始猜测开始执行共轭梯度法的两个步骤：

以便找到系统的近似解决方案。

作为参考，确切的解决方案是：

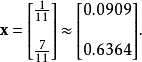
我们的第一步是计算与x0相关的残差向量r0。 该残差由公式r0 = b-Ax0计算，在该情况下等于

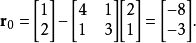
由于这是第一次迭代，我们将使用剩余向量r0作为初始搜索方向p0；选择pk的方法将在进一步的迭代中改变。

我们现在使用关系计算标量α0：

我们现在可以使用公式计算x1：

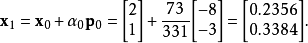
该结果完成了第一次迭代，结果是对系统的“改进”近似解。 我们现在可以使用公式来移动并计算下一个残差向量r1：

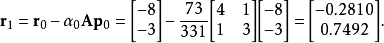
我们的这个过程的下一步是计算最终用于确定下一个搜索方向p1的标量β0。

现在，使用这个标量β0，我们可以使用关系计算下一个搜索方向p1，

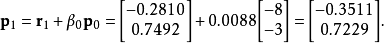
我们现在使用与用于α0的方法相同的方法，使用我们新获取的p1来计算标量α1。

最后，我们使用与用于查找x1相同的方法计算x2。

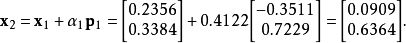
结果x2是系统解决方案中比x1和x0更好的近似值。

如果在该示例中使用精确的算术而不是有限的精度，那么在n = 2次迭代之后（n是系统的顺序）理论上将达到精确的解。