[科普中国]-单侧曲面

基本介绍

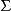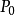在光滑曲面 上任取一点 ，过点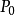 的法线有两个方向，如果选定法线的某个方向为指定的方向，当点在曲面上连续移动时，法线也连续变动、当动点从 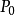出发沿着曲面上任意一条不越过曲面边界的封闭曲线又回到原位置 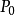时，法线的指向保持不变，称这种曲面为双侧曲面，否则称其为单侧曲面。

单侧曲面是存在的，所谓的莫比乌斯带(Mobius带)就是这类曲面的一个典型例子，如果把一长方形纸条ABCD先扭一次，再粘起来，使A点与C点相合，B点D点相合，这样就可得到它的一个模型。假若用颜色来涂它，那就可以不跨它的边缘而用这种颜色涂遍该带的全部。

详细介绍许多多面体和闭曲面的连通度都是奇数。于是自然会发生这样的问题：有没有连通度为偶数的闭曲面呢?换句话说，有没有按拓扑性质来说，介于球面和环面之间或者介于两个“圈饼”之间的曲面呢?

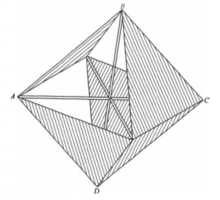
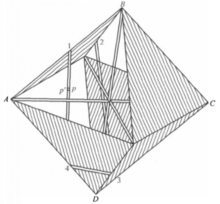
答案是肯定的。可作出一个多面体——七面体，其连通度按多面体的欧拉定理等于2，这些目的，我们从有8个三角形面的正八面体开始(图1)，增添由对角线决定的三个正方形面(例如图1的ABCD)。用这种方法得出含十一个面的图形，它不符合多面体的定义，因为交于每个棱的面数是三个而不是两个，现在我们去掉四个三角形：从图形的前部(按照图1的位置)去掉左上角的三角形和右下角的三角形，从图形的后部去掉左下角的三角形和右上角的三角形，这样一来，只剩下了有阴影线的四个三角形，总共我们得出由四个三角形和三个正方形组成的图形，这图形的棱和顶点是八面体的棱和顶点，但八面体的对角线却不是我们的图形的棱而是面的自交线，显然在每一棱上恰有二面相遇，而且我们可从任一面开始走起，越过若干个棱而达到任一别的面，所以这图形是多面体，由于它有七个面，所以叫做七面体，跟八面体一样，七面体也有十二个棱和六个顶点，由推广的欧拉多面体公式得方程

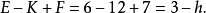
由此得出七面体的连通度h=2，正像简单多面体经过连续变形最后能变成球面一样，七面体经过连续变形也能变成一个简单而闭合的曲面，这种曲面称为“罗马式曲面”，是斯坦纳(Steiner)研究过的，像七面体一样，这种曲面自交于三条相互垂直的线段，它的方程以直角坐标表示时是

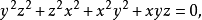可见它是四阶的曲面。

七面体除了有偶数连通度和自交线外，还有此前我们未讨论过的另一重要性质，设想七面体是用薄膜作的，有一个会爬的小动物，例如甲虫，从曲面上的一点P开始爬行，在薄膜的另一侧正对着点P有另一点P’——如果薄膜换成原来的几何曲面，那么P’就和P重合了。可能有人会这样想，甲虫若不在薄膜的某处咬破一个洞就不能从点P爬到点P’，对于球面和一切“圈饼”来说，情形确实是这样的，可是对于七面体来说就不对了。在平行于图2的平面的正方形面朝着观察者的一侧上选择一点P，作为甲虫的出发点(图2)。考虑七面体上从点P出发越过1，2，3，4诸棱又回到原来正方形面的一条道路，显然甲虫从正方形面向前的一侧开始，顺着这条道路爬行，越过标号4的棱到达原正方形面的背后，甲虫当然要在三个地方穿过薄膜，但每次被钻穿的面乃是在七面体自交线上阻碍交通的那个面，而不是甲虫在其上爬行的面。

由于这种理由，七面体称为单侧曲面，而球面和前面讲过的各种“圈饼”称为双侧曲面，此种分类法也适用于有边缘曲面，设想有边缘曲面也是由薄膜制成的，试决定在薄膜上有没有从一侧出发到另一侧的通路，中途不许越过边缘，也不许穿过薄膜。如有这种通路存在，则曲面称为单侧的，否则称为双侧的。圆面等边缘曲面，都是双侧的，但是也可以举出一个比七面体更简单的有边缘的单侧曲面的例子，这就是莫比乌斯带，莫氏带可用一张细长的长方形纸条作成，如图3所示，把两边AB和CD粘起来，使A和C重合，B和D重合，则得到一圆筒形带，如前所述，这是双侧有边缘曲面，另一方面，若在两端黏合之前，把一端相对于另一端扭转180°，然后再使A，D重合，B，D重合，便得到莫比乌斯带的模型(图4)。容易看出，这种曲面是单侧的，因为，在两端黏合之前作一条直线，比方说是PP’，平行于带子的长边，则在两端黏合之后，直线PP’就变为从带子一侧到另一侧的通路QQ’。

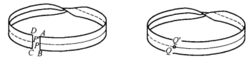
单侧曲面也可以用另一种重要的拓扑概念来刻画，而不必假借曲面是由薄膜制成的，设想任一给定曲面上的每一点(边缘上的点除外，如果有的话)被安全在这曲面上的一条小闭曲线所包围，现在对所有的这些曲线如此规定指向，使充分靠近的二曲线的指向相同，如果规定这样一种行进的指向是可能的，则称这样的一个规定为曲面的一个定向，而曲面称为可定向的。现在我们证明，单****侧曲面不可定向。为了证明，我们考虑和曲面的单侧性等价的一条闭路。比如说，在莫比乌斯带上选好一条道路QQ’，其中的Q和Q’两点还是当做叠合的，让我们给Q指定一个指向，指向既经确定，在整个道路QQ’上就一直沿用它，这样，当动点又来到Q’=Q时，则伴随Q’的指向必同Q的相反，假如莫比乌斯带是可定向的，这种现象便不会发生，所有别种形式的单侧曲面也和莫氏带有类似的情况，反转来也可以证明，所有双侧曲面都是可定向的，由此可知，曲面的双侧与单侧之分，和曲面的可定向与不可定向是一回事。

容易懂得，曲面之不可定向，等价于曲面上存在一条闭曲线s，当圆心在这条曲线上连续运动时，有指向的小圆带着相反的指向回到出发点(例如图4中的曲线QQ’)。在这样的曲面上，沿着曲线s的一侧行进，虽然没有越过曲线，也将达到它的另一侧，由于这种原因，s称为单岸曲线，虽则一个可定向的曲面上所有的曲线都是双岸的，但单岸闭曲线的存在却是不可定向曲面的特征，曲面的单侧性同曲面上存在单岸曲线是等价的。前一性质涉及曲面在空间中的位置，后一性质涉及曲线在曲面上的位置。

七面体有自交线，这一点跟莫比乌斯带不同，那么试问任何单侧闭曲面是不是都自交呢?假如曲面只有一侧，就不可能把空间的一部分同其余的部分分开，即不能把空间分为“内”“外”两部，不自交的闭曲面是不可想象的，事实上，所有单侧闭曲面都要自交，不过这句话的证明，必须另谋途径。

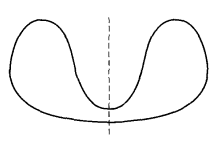
并不是说无论什么曲面的自交都是拓扑性质。例如，考虑图5所画的曲线绕虚线为轴旋转而得的曲面，这一曲面有自交线，即点A所作的圆，但曲面经连续变形，可变成如图6中的曲线所产生的回转曲画，当然这个曲面没有自交线，因此同球面等价。反过来球面也可以经过变形而变为第一个回转曲面，由此可见，自交线的存在不一定就表示拓扑性质。在这个例子里，自交线作成一闭曲线，另一方面，七面体的自交线有六个端点，即七面体的六个顶点，这些点其实应该当做奇点看待，因为曲面上任何正则点的邻域总可经过变形而成为圆面，但对七面体顶点的邻域则不可能这样作(参考图1)，所以七面体有六个奇点，从这里又引出一个问题：有没有无奇点的单侧闭曲面呢?

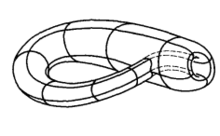
有的，这样的曲面第一次被克莱因发现，我们从一个两头开口的管子出发(图7)，从这种管子可得到环面：把管子弯曲，一直弯曲到两端相遇，然后将两圆口粘在一起。

现在我们改用另一种方法将两端黏合，先将管子的一端捏得比另一端稍细一些，将细的一端掉过头来插入粗的一端的管壁内，使二瓶口作同心圆状(图8)．随后将小口放大，大口缩小，使两口重合在一起，最后把它们粘起来，这样得到的曲面没有任何奇点；它叫做克莱因曲面(也叫做“克莱因瓶”)，其形状如图9．这种曲面显然是单侧的，并且在细端插入管壁处沿一闭曲线自交。

第一个单侧闭曲面的例子——七面体，跟前面讨论过的各种双侧闭曲面不同的地方，在于七面体有偶数的连通度．那么我们可不可以抱着同样的希望，说克莱因瓶的连通度也是偶数的呢?不可以，事实上克莱因瓶的连通度跟环面一样，是3。为了证明，我们也可以像对待环面那样，来选择克莱因瓶的典型截口组，可以选择瓶子两端的接缝作为组中的第一条闭曲线，沿着这条曲线剪开，把曲面拉直使成为圆筒形，然后选择圆筒上的一条母线作为组中的第二条曲线，沿着这条母线将曲面剪开，于是克莱因瓶就变为矩形，像环面一样，再过矩形边缘上任意两点作曲线，曲面就被分成两片了，应用连通度的一般定义于克莱因瓶，可知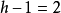 ，故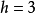 ，这正是我们要证明的。

现在，我们已能以不同的方式叠合矩形(或正方形)的对边，得出五种不同的曲面莫比乌斯带的模型可以从克莱因曲面消去一组对边的叠合关系而得出，因此一定能够把克莱因瓶沿着一条适当选择的闭曲线剪开，使成为莫比乌斯带，图10、11表示用另一种方法把克莱因瓶剪成二条莫氏带，建议读者作出正方形模型的对应演变过程。

在我们讨论过的一些单侧闭曲面里有连通度为偶数的(例如七面体)，也有连通度为奇数的(例如克莱因瓶)；另一方面，我们讲过的一切双侧闭曲面的连通度都是奇数，进一步可以证明，并无连通度为偶数的双侧曲面。

正像正方形一样，一切其他的正4p边多边形也可以用不同的叠合方式由它得出许许多多的曲面模型，其中包括有边缘和无边缘的，单侧和双侧的，如果在图12上的AB和CD是4p边形中将要叠合的二边，则有两种可能的叠合方式：(1)连结对应点的二直线不相变；(2)这样的二直线相交，例如在图12上，第一种情形由叠合A，C而得，第二种情形由叠合B，D而得。现在我们断言：如果4p边形的任意二边是按照第二种方式对应的，则无论其他的边如何对应，所得的曲面永远是单侧的。

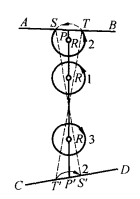
为了证明这句话，即证明多边形所代表的曲面不可定向，设P和P’是在叠合中AB和CD上的二对应点(图12)，那么直线PP’代表曲面上的一条闭路，用R代表在曲面上沿这条路线运动的一点，R先经过P，又由P’回到原处，让我们给曲面上点兄指定一个绕行指向，这个指向在R行进时没有任何不连续的变化，为此我们以R为圆心作一小圆，并以箭头表示它的指向，把小圆随着R连续移动，只要整个圆在4p边形内，它就是多边形代表的曲面上一闭曲线的象，当R接近P时，只有圆弧ST仍留在4p边形内，要想得到曲面上闭曲线的象，必须利用在直线CD上和S，T对应的点S’，T'．但因为AB和CD的叠合是第二类的，S和S’在直线PP'的不同侧，T和T'也如此。这样一来，在曲面上带有绕行指向的闭曲线由二有向弧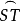 和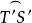 代表，当R达到P然后从P’回到原来位置时这条曲线没有不连续的变化，随着动点R与P’的距离逐渐增加，弧ST逐渐消失，而弧S'T'变为整个圆．但是这圆的指向同原来圆的相反，这就证明了曲面是不可定向的。

作为这个定理的特例，我们得到投影平面是单侧的结论。因为，在投影平面模型里，所有的对应关系都是第二类的。

反转来容易证明，如果所有的对应关系是第一类的，则模型永远代表双侧曲面。

我们已经从球的表面得出投影平面模型，另一方面，我们见过克莱因瓶同环面也有关系，虽然这种关系不同于球面和投影平面的关系，我们现在指出，事实上也可以在克莱因瓶和环面之间建立像球面与投影平面之间一样的对应关系，一般地，对任何单侧曲面，必有一双侧曲面同它对应。

要想从球面得到投影平面，必须把球面的对径点叠合起来，现在我们把类似的做法应用于环面，从环面任一母圆和圆心作环面的轴的垂线，这二直线的交点M叫做环面的中心(图13)，设P是环面上的任一点，则P对于点M的对称点P'也必在环面上，环面上每对对于点M对称的点叫做对径点，把每对对径点看做一点，球面就变成一新的曲面F，今证明F便是克莱因瓶。

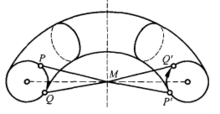
试考虑环面上的一母圆，这母圆对应第二个母圆，如图13所示，二母圆把环面分成两半，曲面F是由去掉环面的一半，并把剩下的一半的边缘圆周上的点如图上指出的方式叠合而成的，相仿地，我们曾经用半球面代替球面来构成投影平面，考虑到二叠合圆的绕行指向，可知半环面由叠合而变成克莱因瓶。

显然第二个半环面可以覆盖在第一个半环面上，使原来的每对对径点现在都重合，但是，这里必须把第二个半环面的里面翻到外面来，像翻手套一样，如果再把这两个半球面粘起来，最后就得双重覆盖的克莱因瓶，由于这种理由，环面可叫做克莱因瓶的双叶覆盖曲面。同理，球面叫做投影平面的双叶覆盖曲面，一般地可以证明，每一单侧曲面有一双侧曲面作为它的双叶覆盖曲面。2