定义
形如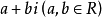 的数叫作复数,其中
的数叫作复数,其中 是复数的实部,b是复数的虚部,全体复数组成的集合叫作复数集,用字母C表示。
是复数的实部,b是复数的虚部,全体复数组成的集合叫作复数集,用字母C表示。
复数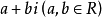 ,当b=0时,就是实数;当b≠0时,叫作虚数;当
,当b=0时,就是实数;当b≠0时,叫作虚数;当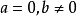 时.叫作纯虚数。
时.叫作纯虚数。
把复数表示成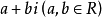 的形式,叫作复数的代数形式。1
的形式,叫作复数的代数形式。1
几何意义从复数相等的定义我们知道,任何一个复数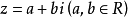 都可以用一个有序实数对(a,b)唯一确定,这样我们可以用建立了直角坐标系的平面来表示复数。
都可以用一个有序实数对(a,b)唯一确定,这样我们可以用建立了直角坐标系的平面来表示复数。
建立了直角坐标系来表示复数的平面叫作复平面,x轴叫作实轴,y轴叫作虚轴,这样,实轴上的点都表示实数,除了原点外,虚轴上的点都表示纯虚数。
复数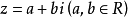 与复平面内的点
与复平面内的点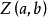 及向量
及向量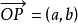 是一一对应的,复数的模表示复数对应的点到原点的距离。1
是一一对应的,复数的模表示复数对应的点到原点的距离。1
判别实数、虚数、纯虚数学习了纯虚数的定义以后,通过这类题来巩固对纯虚数的理解,请看例题.
**例题:**m为何实数时,复数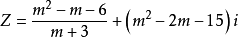 是实数?虚数?纯虚数?
是实数?虚数?纯虚数?
**分析:**要明确什么是复数的实部与虚部?何时它们有意义?何时它们为零或非零?从而由实数、虚数、纯虚数分别对实部与虚部的要求进行讨论。
解:  实部:
实部: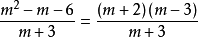 。
。
虚部: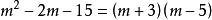 。
。
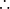 当
当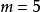 时,Z是实数;
时,Z是实数;
当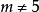 且
且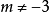 时,Z是虚数;
时,Z是虚数;
当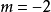 或
或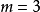 时,Z是纯虚数。
时,Z是纯虚数。
说明:当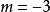 时,实部无意义,在讨论过程中应排除掉。
时,实部无意义,在讨论过程中应排除掉。
**小结:**对这类题可归纳为如下题型。
欲判别复数
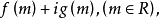 可化为解代数方程或不等式。
可化为解代数方程或不等式。
在实部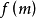 、虚部
、虚部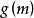 都有定义的前提下:
都有定义的前提下:
实数(对应点在实轴上);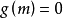 ;
;
虚数(对应点不在实轴上):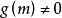 ;
;
纯虚数(对应点在虚轴上):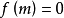 且
且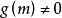 ;
;
对应点在原点:解方程组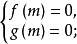
对应点在实轴上方:解不等式
对应点在虚轴左侧:解不等式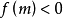 ;
;
对应点在复平面的第一象限内:解不等式组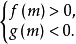
其他情况类推.但应注意所讨论的范围必须在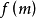 、
、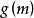 的定义域内。2
的定义域内。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国