[科普中国]-自相关

自相关的含义

给出运用最小二乘法的假设条件：

(1)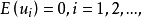 ，即扰动项均值为零；

(2)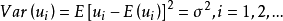 ，即常数方差或同方差性；

(3)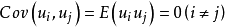 ，即各观测值扰动项相互独立或互不相关；

(4)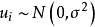 ，即扰动项的正态性； 其中第(3)条 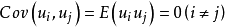保证的即是模型中扰动项 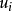之间不存在相关关系，当 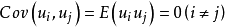时，则线性回归模型的扰动项 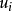存在自相关。

自相关在计量经济学中主要指的是回归模型中不同观测值其扰动项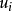 之间的相关关系。自相关问题通常与时间序列数据有关，所以自相关也称为序列相关；如果是由截面数据产生的自相关问题，则称为空间相关。1

自相关的类型通常情况下，自相关可以分为两类。

一阶自回归形式即扰动项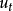 只与其滞后一期值有关的情况,即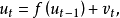则称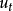 具有一阶自回归形式。

高阶自回归形式即扰动项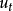 在本期的值不仅与其前一期滞后值有关，还与其前若干期的滞后值都相关的情况，

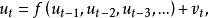则称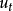 具有高阶自回归形式。

一般来说，计量经济模型中常见的自相关为一阶自回归形式。1

自相关的假定在一阶自回归的形式下来讨论自相关的相关假定。通常假定扰动项的自相关是线性的，即

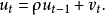
其中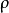 是自回归系数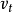， 是随机扰动项，且 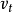满足以下假设：

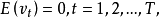
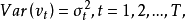
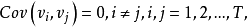
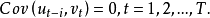
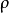的取值范围为[一1，1]：

当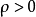 时，称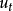 存在正相关；

当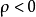 时，称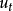 存在负相关；

当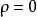 时，称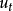 不存在相关关系。

自相关产生的原因和后果产生自相关的原因1．惯性

即冲击的延期影响，大多数经济时间序列都存在自相关。例如GNP就业、货币供给、价格指数等，随机扰动的影响往往会持续一段时间，而不仅仅是一个取值时期。当处于经济恢复周期时，由萧条的底部开始，大多数经济序列的数据都会向上浮动，序列某一时点之后的取值会大于其各个前期的取值，这就是一种冲击的延期影响。其他的例子如地震、洪水等偶发的外部因素改变，通常也会造成某一段时间内的数据发生整体的偏移。但是随着观测时期的延长，这种冲击造成的滞后影响会逐渐消退。

2．模型设定误差

如果模型所选用的函数形式与实际变量之间的真实关系不相符，随机扰动项往往会存在自相关。例如当被解释变量与解释变量之间应为对数关系，而模型却选用线性回归来进行拟合，那么该回归模型必存在自相关。

3．略去了带有自相关的解释变量

在建立计量经济模型时，我们往往会选择最重要的几个解释变量，而将次要的解释变量略去，如果被略去的解释变量本身存在自相关，它必然在随机扰动项中反映出来。但有时由于多个被略去的解释变量之间的自相关关系会相互抵消，而使得模型表现为非自相关。1

自相关的后果若随机扰动项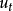 存在自相关时，会对回归结果造成以下影响。

(1)回归系数最小二乘估计仍然是线性和无偏的。

(2)回归系数最小二乘估计不再是有效的。

(3)可能低估扰动项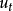 的方差。

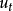(4)由于回归系数估计值 的方差以及扰动项 的方差被低估，导致OLS方法计算得到的拟合优度 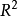不能反映模型的真实 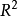；同时导致根据被低估的 方差所计算的预测区间不可靠。1

自相关的解决方法**(一)变换模型的数学形式**

如果造成自相关的原因是错误地设定了模型中的数学形式，导致无法正确反映经济变量的真实情况，此时适当的方法就是改变初始的线性形式，使用其他数学形式进行估计，并重新检验在新的形式下所得残差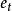 ，如果此时不存在自相关，则认为该数学形式便是合适的模型。

(二)将自相关的变量引人模型中

如果造成自相关的原因是由于略去了具有自相关的解释变量，那么合适的处理方法是将这些被错误略去的解释变量重新引人模型中去。例如，在消费函数中，t期的消费不仅取决于t期的收人，还取决于前一期的收入水平，如果查明自相关性是由于略去的前一期收入水平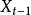 引起的，则只要将前一期收入 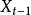作为解释变量加入模型，模型中的自相关就会消除。即

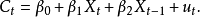其中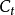， 表示t期的消费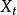； 表示t期的收入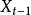； 表示前一期的收入。

(三)广义差分法

当上述两种来源的自相关消除后，就可以认为模型中仍然存在的自相关主要来源于随机扰动项本身。在这种情况下，对于一阶自相关的形式，解决的办法是变换原回归模型，通过变换消除随机扰动项中的自相关，白相关消除后再利用普通最小二乘法估计回归参数，这种估计方法称广义差分法。

自相关的参数估计以上介绍的用于消除自相关的广义差分法，若不知道 的取值，那么还要进一步分析。

以下介绍两种估计 的方法。

(一)利用DW统计量估计

由DW检验法已知： 。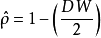

首先利用残差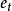 求出DW统计量的值，然后利用上式求出自相关系数 的估计值，但由于运用此方法需要用到DW统计量，因此样本容量应较大。

**(二)**达宾(Durbin)两步法

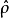达宾(Durbin)两步法的基本原理为：①计算自相关系数 的估计值 ；②利用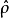 进行广义差分变换，然后对变换后的模型运用最小二乘法估计参数。