概念
定义1:设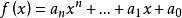 是整系数多项式,称
是整系数多项式,称
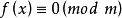 是关于未知数
是关于未知数 的模
的模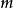 的同余方程,简称为模
的同余方程,简称为模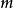 的同余方程。
的同余方程。
若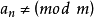 ,则称
,则称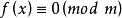 为
为 次同余方程。
次同余方程。
定义2:设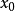 是整数,当
是整数,当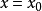 时,
时,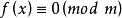 成立,则称
成立,则称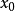 是同余方程
是同余方程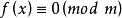 的解。凡对于模
的解。凡对于模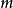 同余的解,被视为同一个解。同余方程
同余的解,被视为同一个解。同余方程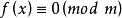 的解数是指它的关于模
的解数是指它的关于模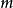 互不相余的所有解的个数,也即在模
互不相余的所有解的个数,也即在模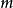 的一个完全剩余系中的解的个数。
的一个完全剩余系中的解的个数。
由定义2,同余方程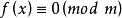 的解数不超过
的解数不超过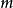 。1
。1
基本原理定理:下面的结论成立:
(1)设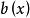 是整系数多项式,则同余方程
是整系数多项式,则同余方程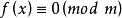 与
与
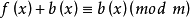 等价;
等价;
(2)设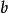 是整数,
是整数,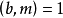 ,则同余方程
,则同余方程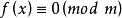 与
与
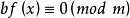 等价;
等价;
(3)设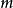 是素数,
是素数,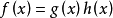 ,
,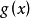 与
与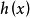 都是整系数多项式,又设
都是整系数多项式,又设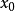 是同余方程
是同余方程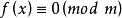 的解,则
的解,则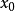 必是同余方程
必是同余方程
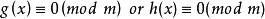 的解。
的解。
证明:(1)若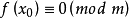 ,则
,则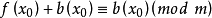 成立,反之,若
成立,反之,若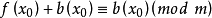 ,则
,则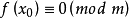 成立;
成立;
(2)若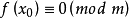 ,则
,则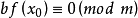 成立,反之,若
成立,反之,若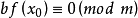 ,则由
,则由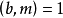 得
得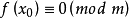 成立;
成立;
(3)若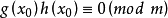 ,则由
,则由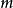 是素数得
是素数得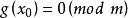 或
或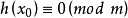 。证毕。1
。证毕。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国