概念奇异边界法是与基本解法相对应的一种边界型无网格数值离散方法。该方法提出了源点强度因子的概念,克服了传统基本解方法中最复杂最头疼的虚拟边界问题。基于边界元法中处理奇异积分的数值处理技术, 导出了源点强度因子的解析表达式, 提出了改进的无网格奇异边界法, 并进一步将该方法应用于三维位势问题。该方法消除了传统方法中样本点的选取, 在不增加计算量的前提下, 极大地提高了奇异边界法的计算精度与稳定性。
基本原理奇异边界法的近似格式本文以二维Helmholtz方程为例描述奇异边界法的基本技术路线:
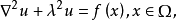
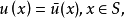 其中
其中 是待求未知量,
是待求未知量,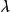 为波数,
为波数, 是空间坐标,
是空间坐标,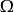 和
和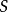 分别代表计算域及其边界,
分别代表计算域及其边界,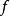 和
和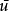 为已知函数。二维Helmholtz方程的基本解是
为已知函数。二维Helmholtz方程的基本解是
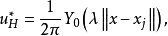 这里
这里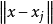 代表
代表 和
和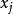 两点间的欧几里得距离。
两点间的欧几里得距离。
根据基本解法的原理,以基本解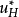 为插值基函数,Helmholtz方程
为插值基函数,Helmholtz方程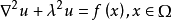 的待求函数可以近似为
的待求函数可以近似为
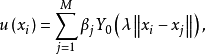 其中
其中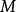 是边界离散点的数目,
是边界离散点的数目,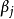 为待求插值系数。当配点
为待求插值系数。当配点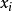 和源点
和源点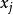 重叠时,
重叠时,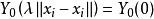 不存在,即产生原点奇异性。为了避免基本解的奇异性,基本解方法的策略是将源点
不存在,即产生原点奇异性。为了避免基本解的奇异性,基本解方法的策略是将源点 虚拟地布置在物理域以外的虚假边界上,而将配点
虚拟地布置在物理域以外的虚假边界上,而将配点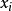 布置在真实的物理边界上,即插值源点和配点是两组完全不同的点。但到目前为止,对于复杂几何域或多连通几何域问题,如何较好地布置虚拟源点
布置在真实的物理边界上,即插值源点和配点是两组完全不同的点。但到目前为止,对于复杂几何域或多连通几何域问题,如何较好地布置虚拟源点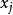 以保证计算结果可靠和稳定收敛,仍是基本解方法中一个未能解决的关键问题。
以保证计算结果可靠和稳定收敛,仍是基本解方法中一个未能解决的关键问题。
奇异边界法不同于基本解方法的关键之处在于,插值源点 和配点
和配点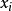 是同一组物理边界的离散点,因而不存在基本解方法中的虚假边界选取问题。奇异边界法的插值公式为:
是同一组物理边界的离散点,因而不存在基本解方法中的虚假边界选取问题。奇异边界法的插值公式为:
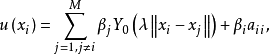 这里
这里 是插值点的总数,
是插值点的总数,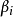 是待定插值系数。值得注意的是,插值公式
是待定插值系数。值得注意的是,插值公式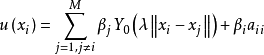 和
和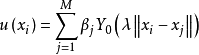 都用基本解为基函数,但插值公式
都用基本解为基函数,但插值公式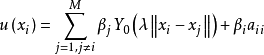 在配点
在配点 和源点
和源点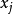 重合处,假设了一个源点强度因子(origin intensity factor)
重合处,假设了一个源点强度因子(origin intensity factor)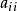 。
。
将插值公式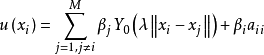 代入方程
代入方程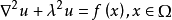 和
和 ,令
,令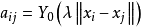 ,因为基本解满足控制方程,我们得到下面矩阵形式的边界条件离散代数方程:
,因为基本解满足控制方程,我们得到下面矩阵形式的边界条件离散代数方程:
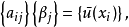 源点强度因子
源点强度因子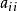 实际上是插值矩阵
实际上是插值矩阵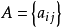 的对角线元素。由于基本解的原点奇异性,我们不能够简单地用基本解插值基函数来计算
的对角线元素。由于基本解的原点奇异性,我们不能够简单地用基本解插值基函数来计算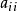 。理想的方法是从数学理论上导出一个计算源点强度因子的公式,但目前这是一个非常有挑战性的数学物理问题。下面我们通过反插值技术来求解源点强度因子
。理想的方法是从数学理论上导出一个计算源点强度因子的公式,但目前这是一个非常有挑战性的数学物理问题。下面我们通过反插值技术来求解源点强度因子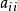 。
。
反插值技术注意到插值公式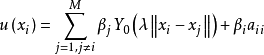 和离散代数方程
和离散代数方程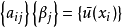 中的待求插值系数
中的待求插值系数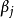 与边界上的配点分布,边界条件和右边项有关,而源点强度因子
与边界上的配点分布,边界条件和右边项有关,而源点强度因子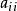 仅依赖于边界条件和边界上的配点分布,与右边项无关。因而,我们可以设计一个反插值技术来计算对角线元素。
仅依赖于边界条件和边界上的配点分布,与右边项无关。因而,我们可以设计一个反插值技术来计算对角线元素。
对方程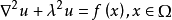 和
和 所描述的Helmholtz有限域问题,在其物理域的边界上布置
所描述的Helmholtz有限域问题,在其物理域的边界上布置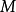 个配点
个配点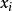 ,在物理域内部布置
,在物理域内部布置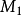 个计算辅助点
个计算辅助点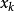 。对于有基本解的控制方程,容易发现它们的一些已知特解。对Helmholtz方程,有许多已知的简单特解,例如
。对于有基本解的控制方程,容易发现它们的一些已知特解。对Helmholtz方程,有许多已知的简单特解,例如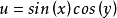 。利用插值公式
。利用插值公式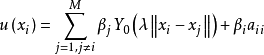 ,我们有
,我们有
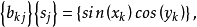 这里
这里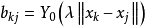 ,
,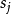 是
是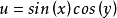 在边界配点
在边界配点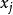 上的影响系数。因为辅助点
上的影响系数。因为辅助点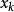 和配点
和配点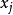 完全不重叠,因而没有奇异性问题。由方程
完全不重叠,因而没有奇异性问题。由方程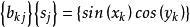 ,我们就可以求得影响系数
,我们就可以求得影响系数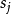 。
。
这里内部辅助点 的个数可以等于或多于边界配点
的个数可以等于或多于边界配点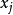 的数目。本文中采取两种方案:
的数目。本文中采取两种方案:
方案1——在物理区域内部布置与边界配点相等数目的辅助点(即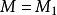 ),可以得到
),可以得到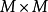 插值方阵;
插值方阵;
方案2——在物理区域内部布置辅助点的数目多于边界配点数(即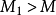 ),可以得到
),可以得到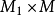 插值矩阵,需用移动最小二乘近似求解。
插值矩阵,需用移动最小二乘近似求解。
下一步,我们将计算辅助点换成边界源点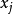 ,即配点和源点完全重叠在边界上;我们有
,即配点和源点完全重叠在边界上;我们有
 这里插值矩阵
这里插值矩阵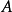 的非对角线元素可由公式
的非对角线元素可由公式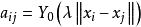 得到。因而利用方程
得到。因而利用方程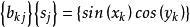 中求得的系数
中求得的系数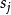 ,我们就能用方程
,我们就能用方程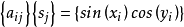 计算出关键的未知对角元素
计算出关键的未知对角元素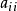 ,即源点强度因子。
,即源点强度因子。
利用上面得到的源点强度因子,我们就可以用边界插值公式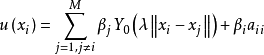 ,计算具有相同几何形状和控制方程的任意问题。1
,计算具有相同几何形状和控制方程的任意问题。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国