[科普中国]-函数关系

定义

设A和B是两个给定的集合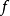， 是从集合A到集合B的一个二元关系。如果这个二元关系还满足下面的性质：对每个元素 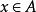，存在唯一的元素 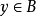，使得二元序偶 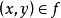，就称这个二元关系是从集合A到集合B的一个函数或者映射。记作

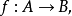或者

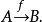
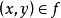也可改写为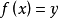 ，其中y称为x的象，而x则称为y的原象。称集合A是函数的定义域，集合A中所有元素在函数 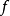的作用下得到的所有象的集合称为函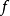数 的象或函数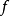 的值域。2

为了进一步区分不同特性的函数，给出细分的定义。

设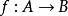 是从集合A到集合B的一个函数。

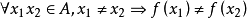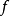(1)如果 ，则称函数 是从集合A到集合B的一个单射。

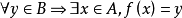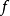(2)如果 ，则称函数 是从集合A到集合B的一个满射。

(3)如果函数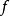 既是从集合A到集合B的一个单射．又是从集合A到集合B的一个满射，则称它是从集合A到集合B的一个双射。2

注意点关于函数定义的几点说明：

(1)如果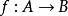 是从集合A到集合B的一个函数，那么集合A中每个元素必须都有象，且象必须唯一。

(2)如果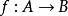 是从集合A到集合B的一个函数．那么集合B中每个元素不一定都有原象，且当有原象时，原象也不一定唯一。

(3)根据函数的定义可知，两个函数是否相等。需要看：二者的定义域是否相同；对于定义域内的每一个元素．它在这两个函数作用下的象是否恒相同。2

函数关系的建立方法步骤对于实际问题，明确其中各种量及量之间的关系，建立正确的函数关系十分重要。在建立函数关系时，首先要确定问题中的自变量与因变量，再根据它们之间的关系列出等式，得出函数关系式，然后确定函数定义域，确定定义域时，不仅要考虑到函数关系的解析式，还要考虑到变量在实际问题中的含义。3

建立函数关系的基本步骤：

①明确问题中的因变量与自变量，并以适当记号表示；

②寻找等量关系，建立函数关系；

③确定函数的定义域。

举例说明下面举例说明如何建立函数关系。

例1 某商场销售某种商品8000件，每件原价70元，当销售量在5000件以内(包含5000件)时，按照原价出售，超过5000件部分，打八折销售。试建立总销售收入与销售量之问的函数关系。

**解：**设销售量为x件，总销售收入为R元，总销售收人与销售量之间的函数关系为

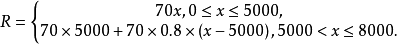
例2 某工厂生产某种型号的车床，年产量为a台，分若干批次进行生产，每批次的生产准备费为b元，设产品均匀投入市场，且上一批用完后立即生产下一批，即平均库存量为批量的一半，设每年每台库存费为c元，显然，生产批量大则库存费高；生产批量少则批数增多，因而生产准备费高，为了选择最优批量，试求出一年中库存费与生产准备费的和与批量之问的关系。

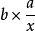**解：**设批量为x，库存费与生产准备费的和为P(x)，因年产量为a，所以每年生产的批数为 (设其为整数)，则生产准备费为 ，因库存量为a，故库存费为 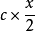，因此可得

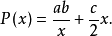定义域为(0，a]，因本题中的x为车床的台数，批数 为整数，所以x只应取(0，a]中的a的正整数因子。

例3 某牧场要建造占地100m2的矩形围墙，现有一排长20m的旧墙可供利用，为了节约投资，矩形围墙的一边直接用旧墙修，另外三边尽量用拆去的旧墙改建，不足部分用购置的新砖新建，已知整修1m旧墙需24元，拆去1m旧墙改建成1m新墙需100元，建造1m新墙需200元，设旧墙所保留的部分用x表示，整个投资用y表示，将y表示为x的函数。

**解：**整个投资的费用包括整修旧墙的费用、拆旧改新的费用以及建造新墙的费用，所以所求函数关系为

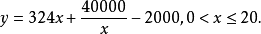
例4 某地区上年度电价为0.8元/(kW·h)，年用电量为a kW·h，本年度将电价降到0.55元/(kW·h)至0.75元/(kW·h)之间，而用户期望电价为0.4元/(kW·h)，经测算，下调电价后新增的用电量与实际电价和用户期望电价的差成反比(比例系数为k)，该地区的电力成本为0.3元/(kW·h)，写出本年度电价下调后，电力部门的收益y与实际电价x的函数关系式。3

**解：**收益=实际用电量×(实际电价-成本价)。

所以所求函数关系式为

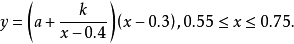
几类常见的函数关系模型一次函数模型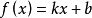(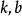为常数，).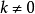

反比例函数模型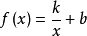(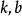为常数，).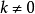

二次函数模型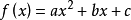(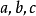为常数，).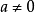

指数型函数模型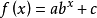(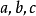为常数，，).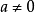

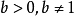对数型函数模型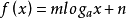(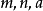为常数，，).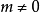

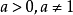幂型函数模型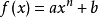(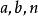为常数，).4

函数关系与相关关系的区分相关关系的定义当变量X取某个值时，变量Y的取值可能有若干个，这些数值表现为一定的波动性，但总是围绕着它们的平均数，并遵循一定的规律变动。变量之间存在的这种不确定的数量关系称为相关关系。特点：Y与X的值不一一对应；Y与X的关系不能用函数式严格表达，但有规律可循。

例如：父亲身高Y与子女身高X之间的关系；收入水平Y与受教育程度X之间的关系；粮食亩产量Y与施肥量X1、降雨量X2、温度X3之间的关系；商品的消费量Y与居民收入X之间的关系；商品销售额Y与广告费支出X之间的关系。1

二者的的区分区分相关关系与函数关系的依据全凭因变量取值的确定性：若因变量的取值是确定的、唯一的，则两个变量之间的关系称为函数关系；若因变量的取值是不确定的，则两个变量之间的关系称为相关关系。

例5 试判定下列变量之间属于函数关系，还是相关关系。

(1)圆面积与圆半径 (2)价格确定下商品的销售额与销售量

(3)人们的身高与体重 (4)商品广告费支出与销售额

(5)家庭月收入与月支出 (6)施肥量与亩产量

(7)文化程度与年收入 (8)图书印数与图书价格

(9)商品销售额与商品流通费用率 (10)可变销售价格与商品销售额

**解：**按照函数关系和相关关系的定义与区别，本例中，第(1)、第(2)为函数关系，其余均为相关关系。

**注意：**变量之间的函数关系和相关关系在一定条件下是可以相互转化的。本来具有函数关系的变量，在存在观测误差时，其函数关系往往以相关的形式表现出来。而具有相关关系的变量之间的联系，如果对其有深刻的规律性认识，并且能够把影响因变量变化的因素全部纳入方程，这时相关关系也可能转化为函数关系。另外，相关关系也具有某种变动规律性，所以，相关关系经常可以用一定的函数形式去近似地描述。客观现象的函数关系可以用数学分析的方法研究，而研究客观现象的相关关系，则必须借助于统计学中的相关与回归分析方法。1