概念
如果在两条曲线之间可以建立一个点对应,使得在对应点这两条曲线有公共的主法线,则称这两条曲线为共轭曲线。如果一条曲线有不与自身重合的共轭曲线,则称其为Bertrand曲线。互为共轭的曲线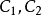 之间距离为常数,且在对应点间的切线成定角。
之间距离为常数,且在对应点间的切线成定角。
设计共轭曲线机构的图解法包络法已知实现给定运动规律的瞬心线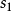 、
、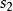 及共轭曲线中的一条曲线
及共轭曲线中的一条曲线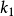 ,求
,求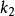 。这相当于由
。这相当于由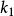 、
、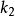 求
求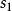 、
、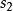 的逆过程。
的逆过程。
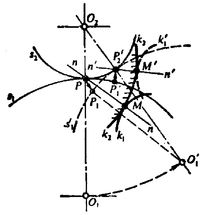
设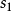 相对
相对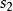 滚动(图1),其角速度分别为
滚动(图1),其角速度分别为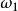 、
、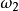 ,应用反转法,给整个机构绕
,应用反转法,给整个机构绕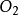 的反转角速度
的反转角速度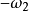 ,则
,则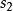 固定,
固定,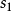 沿
沿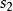 滚动,如图1表示
滚动,如图1表示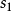 连同
连同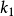 滚到
滚到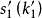 、
、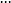 等位置。此时:
等位置。此时: ,与
,与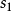 固结的
固结的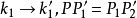 。
。
设想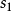 沿
沿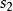 滚动至无数点接触,相应地有无数条曲线
滚动至无数点接触,相应地有无数条曲线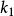 、
、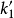 、
、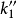 、
、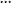 ,这些
,这些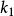 曲线的包络线即为曲线
曲线的包络线即为曲线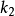 。由此可知,已知
。由此可知,已知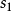 、
、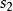 和共轭曲线
和共轭曲线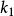 、
、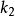 中的一条,可利用包络原理求出与其共轭的另一条,故共轭曲线机构常称为包络线机构。注意图1中法线
中的一条,可利用包络原理求出与其共轭的另一条,故共轭曲线机构常称为包络线机构。注意图1中法线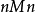 过点
过点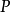 、
、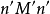 过点
过点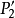 、
、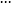 ,
,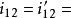 常值。
常值。
法线法设给定瞬心线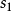 、
、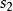 的中心距
的中心距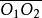 、传动比
、传动比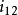 及共轭曲线中的一条曲线
及共轭曲线中的一条曲线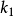 ,求作啮合线及
,求作啮合线及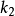 。
。
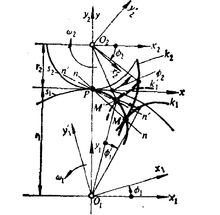
如图2,建立三个坐标系:定坐标系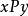 或
或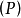 ,分别与
,分别与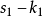 、
、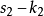 一起转动的动坐标系
一起转动的动坐标系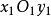 或
或 、
、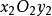 或
或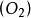 三个坐标的始位相互平行。起始时
三个坐标的始位相互平行。起始时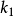 上点
上点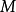 进入啮合,法线
进入啮合,法线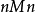 过点
过点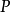 。设
。设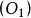 转过角
转过角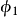 ,由
,由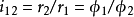 可知
可知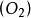 转过
转过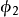 ,此时
,此时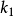 转到图示的
转到图示的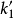 ,
,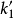 的法线
的法线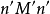 亦过点
亦过点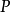 ,故点
,故点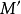 进入啮合。
进入啮合。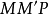 为啮合点画在
为啮合点画在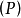 上的轨迹,称为啮合线;
上的轨迹,称为啮合线;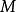 、
、 、
、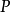 等啮合点画在动坐标系
等啮合点画在动坐标系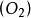 上的轨迹即为所求曲线
上的轨迹即为所求曲线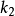 ,图示
,图示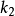 为始位。注意
为始位。注意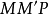 等啮合点画在
等啮合点画在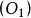 上的轨迹就是曲线
上的轨迹就是曲线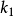 。1
。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国