雅可比椭圆函数的定义
雅可比椭圆函数有十二种,各对映到某个矩形的顶点连线。此诸顶点记作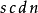 。
。
视此矩形为复数平面的一部分, 是原点,
是原点, 是实轴上的一点
是实轴上的一点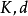 是
是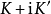 ,
, 是
是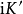 。
。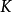 与
与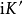 称作四分之一周期。
称作四分之一周期。
十二个椭圆函数分别记为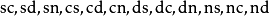 。为方便起见,取变数
。为方便起见,取变数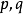 意指矩形上的任一对顶点,则函数
意指矩形上的任一对顶点,则函数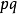 是满足以下性质的周期亚纯函数:
是满足以下性质的周期亚纯函数:
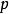 是单零点,
是单零点,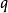 是单极点。
是单极点。
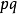 在
在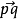 方向的周期等于
方向的周期等于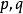 距离的两倍。对另两个从
距离的两倍。对另两个从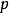 出发的方向,
出发的方向,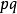 亦满足同样性质。
亦满足同样性质。
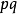 在顶点
在顶点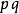 的展式首项系数均为一。
的展式首项系数均为一。
表列如次:
|| ||
一般而言,须以平行四边形代替上述矩形,以考虑更一般的周期。
雅可比椭圆函数的性质特殊点的值
|| ||
sn(mK+niK±z)诱导公式表
|| ||
cn(mK+niK±z)
|| ||
dn(mK+niK±z)
|| ||
基本关系
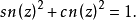
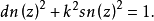
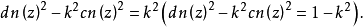
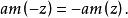
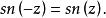
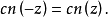
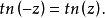
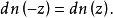
可见,雅可比椭圆函数的关系与圆函数(三角函数)相似1。
加法定理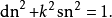 由此可见 (cn,sn,dn) 描出射影空间
由此可见 (cn,sn,dn) 描出射影空间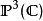 中两个二次曲面之交,这同构于一条椭圆曲线。曲线上的群运算由下列加法公式描述:
中两个二次曲面之交,这同构于一条椭圆曲线。曲线上的群运算由下列加法公式描述:
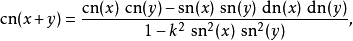
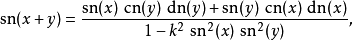
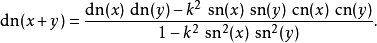
函数的平方之间的关系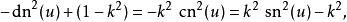
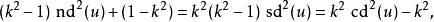
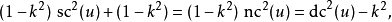
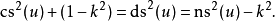
反函数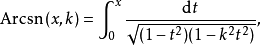
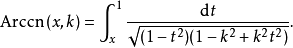
用Θ函数来定义雅可比椭圆函数也可以用Θ函数来定义。如果我们把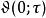 简写为
简写为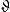 ,把
,把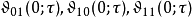 分别简写为
分别简写为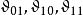 (Theta常数),那么椭圆模k是
(Theta常数),那么椭圆模k是 。如果我们设
。如果我们设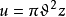 ,我们便有2:
,我们便有2:
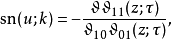
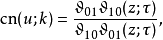
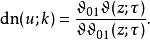
常微分方程的解[编辑]三个基本的雅可比椭圆函数的导数为:
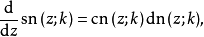
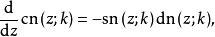

根据以上的加法定理,可知它们是以下非线性常微分方程的解3:
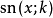 是微分方程
是微分方程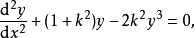 和
和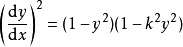 的解;
的解;
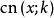 是微分方程
是微分方程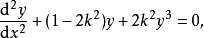 和
和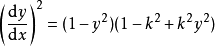 的解;
的解;
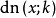 是微分方程
是微分方程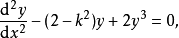 和
和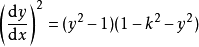 的解4。
的解4。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国