定义
有向直线,简而言之,就是规定了正方向的直线。如数轴,直角坐标系中的x轴、y轴,都叫做有向直线。
任意一条直线,都可以规定两个相反的方向,如果把其中的一个方向作为正方向,那么相反的方向就是负方向,像这样规定了正方向的直线叫做有向直线。2
如果给直线定一个正向,则它叫做有向直线。有向直线上的线段也“有向”,若A、B是直线上两个不同的点,以A为始点以B为终点的矢量就是一个有向线段,它的正向可以和直线正向相同或相反,但是如果不和直线相联系,空间一个非零矢不能叫做有向线段。
用矢量的话说,已给一条直线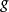 和与
和与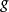 共线的非零矢
共线的非零矢 ,则若以
,则若以 的方向为
的方向为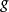 的正向,则有向直线
的正向,则有向直线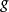 与
与 同方向,
同方向, 叫做有向直线的定向矢,直线
叫做有向直线的定向矢,直线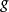 上的矢量或有向线段,不是与
上的矢量或有向线段,不是与 同向就是与
同向就是与 反向。3
反向。3
记法有向直线是规定了正方向的直线。直角坐标系中的 轴、
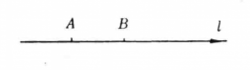
轴、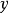 轴都是有向直线。表示有向直线,可顺着直线的正向依次取两点A、B,记为有向直线AB,也可以在箭头的旁边写一个拉丁字母
轴都是有向直线。表示有向直线,可顺着直线的正向依次取两点A、B,记为有向直线AB,也可以在箭头的旁边写一个拉丁字母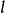 ,记为有向直线
,记为有向直线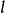 。4
。4
直线上矢量的代数长有向直线上的矢量或有向线段不仅有长度还有表示方向的符号,当有向直线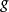 上的非零矢
上的非零矢 和
和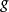 同向时,
同向时, 的长度前加正号,即|
的长度前加正号,即| |;当
|;当 的方向和
的方向和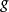 的相反时,加负号,即-|
的相反时,加负号,即-| |,我们把
|,我们把 的带符号的长度叫做
的带符号的长度叫做 的代数长。矢量
的代数长。矢量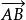 的代数长用
的代数长用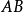 表示,显然
表示,显然 ,我们也用记号
,我们也用记号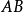 表示有向线段而不会引起混淆。
表示有向线段而不会引起混淆。
直线上的矢量相加,设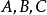 为同一直线上三个点,无论
为同一直线上三个点,无论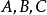 怎样排列,我们知道,总有关系
怎样排列,我们知道,总有关系
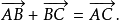 当我们作图表示时,也可以看出:不论
当我们作图表示时,也可以看出:不论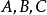 有怎样的相互位置,它们的代数长也有类似的公式,
有怎样的相互位置,它们的代数长也有类似的公式,
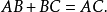
我们还必须注意,空间中的矢量只有它在一条有向直线上才有所谓的代数长,零矢的代数长是零。3




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国