定义
当两条直线相交所构成的四个角中,如果有一个角是直角,就称这两条直线互相垂直,其中一条直线叫做另一条直线的垂线(垂直线),它们的交点叫做垂足。两条直线互相垂直,是两条直线间又一重要的位置关系。
证明两直线垂直的方法说明证明两条直线互相垂直的方法很多,现列出十种主要方法如下:
1.直接用定义。即证相交两直线所构成的角中有一个是直角,或通过计算,求出其中的一个角等于90°。
2.如果一三角形中,有两个内角之和等于90°,那么这个三角形是直角三角形。
3.一条直线垂直于平行线中的一条,则这条直线也垂直于平行线中的另一条直线。
4.利用等腰三角形“三线合一”的性质,即等腰三角形底边上的中线、高和顶角的平分线互相重合。
5.利用勾股定理逆定理。即在△ABC中,如果它的三条边 有关系式
有关系式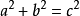 ,那么∠C=90°(这个三角形是直角三角形)。
,那么∠C=90°(这个三角形是直角三角形)。
6.利用菱形的性质,即菱形的两条对角线互相垂直平分。
7.利用垂径定理及其逆定理。例如,在圆O中,P是弦AB的中点,连结OP,则OP⊥AB。
8.利用圆周角定理的推论。即在圆中,直径所对的圆周角是直角,或半圆所对的圆周角等于90°。
9.利用定理:在三角形中,如果一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
10.利用切线的性质定理:圆的切线垂直于过切点的半径。
除了上述十种主要方法外,还有一些其他方法。例如,利用线段垂直平分线性质的逆定理,即如果一点到线段两端点的距离相等,那么这一点必在这条线段的垂直平分线上。也可以利用三角函数的计算来证明两直线垂直。例如,当角a是锐角时,如果sina=1,那么a=90°(当然,由cosa=0,或ctga=0,同样可推得a=90°)。总之,证明两条直线互相垂直的方法很多,读者在运用时既要根据所给条件或图形的特征,灵活选择方法,同时辅以必要的分析与综合,一定能较简捷地证明两条直线互相垂直。1
例题解析例1 如图1,在△ABC的外侧以AB、AC为斜边分别作等腰直角三角形ABD、ACE。设BC的中点为O,连结DO、EO,求证DO⊥EO且DD=EO。
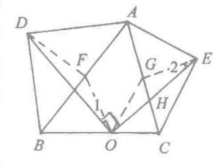
分析: 利用等腰直角三角形的性质,取AB、AC的中点F、G,连结DF、FO、EG、GO。由三角形中位线性质,可得到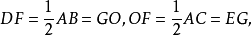 且
且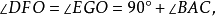 于是可得
于是可得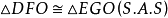 ,有
,有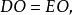 且
且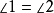 。但
。但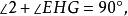 而
而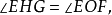 从而得到
从而得到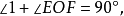 即
即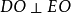 。
。
(请读者自己完成证明过程。)
在本题中,由于中点较多,所以首先从三角形中位线性质去考虑。同时,本题是直接证得∠DOE=90°。从而有DO⊥EO的结论。
例2 如图2,△ABC中,已知AB=AC,且BM⊥AC,CN⊥AB(M、N为垂足),又O、P分别是BC、MN的中点。求证:OP⊥MN。
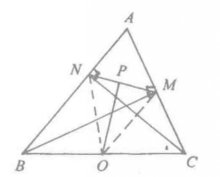
分析一: 利用直角三角形斜边上中线的性质,容易得到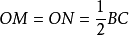 。这样,△OMN是一个等腰三角形,因为P是底
。这样,△OMN是一个等腰三角形,因为P是底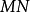 的中线,即得OP⊥MN。
的中线,即得OP⊥MN。
分析二: 从已知∠BNC=∠BMC=90°,易证B、C、M、N四点共圆,圆心即点O。这样,线段MN是该圆的一条弦。因为P为MN中点,由垂径定理逆定理,即得OP⊥OM。
本题告诉我们,在证两条直线互相垂直时,要认真审题,看清图形特征,从而选择适当的方法。需要时也可一题多证,以培养发散思维及证题能力。1
坐标系中垂直关系的证明说明两直线垂直的充要条件:不与x轴垂直的两条直线的斜率互为负倒数。
例题解析**例1:**设直线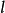 过点M(3,2),且与直线
过点M(3,2),且与直线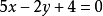 垂直,求直线
垂直,求直线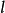 的方程。
的方程。
 **解:**直线
**解:**直线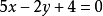 的斜率为
的斜率为 ,
,
 直线
直线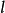 的斜率为
的斜率为 ,
,
故直线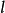 的方程为
的方程为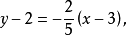 整理得
整理得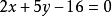 。
。
另外,两条直线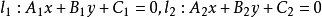 互相垂直的充要条件是:
互相垂直的充要条件是: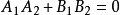 。
。
**例2:**直线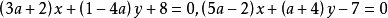 互相垂直,求a的值。
互相垂直,求a的值。
解:
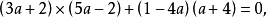
解得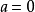 或
或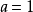 。
。
另外与直线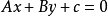 (
(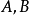 不同时为0)垂直的直线系方程为
不同时为0)垂直的直线系方程为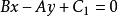 。
。
例1也可这样解: 与直线
与直线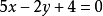 垂直的直线系方程为
垂直的直线系方程为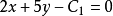 ,直线过点M(3,2),
,直线过点M(3,2),
所以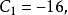 因此,所求的直线为
因此,所求的直线为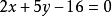 。2
。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国