[科普中国]-正规方程

概述

为了获得更可靠的结果，测量次数 总要多于未知参数的数目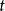 ，即所得误差方程式的数目总是要多于未知数的数目。因而直接用一般解代数方程的方法是无法求解这些未知参数的。最小二乘法则可以将误差方程转化为有确定解的代数方程组（其方程式数目正好等于未知数的个数），从而可求解出这些未知参数。这个有确定解的代数方程组称为最小二乘法估计的正规方程（或称为法方程）。

线性参数的最小二乘法处理程序可归结为：首先根据具体问题列出误差方程式；再按最小二乘法原理，利用求极值的方法将误差转化为正规方程；然后求解正规方程，得到待求的估计量；最后给出精度估计。对于非线性参数，可先将其线性化，然后按上述线性参数的最小二乘法处理程序去处理。因此，建立正规方程是待求参数最小二乘法处理的基本环节。1

等精度测量线性参数线性参数的误差方程式为

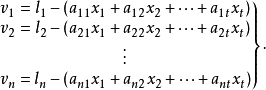
在精度测量中，应满足最小二乘条件式，即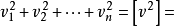： 最小。

现求上式子的估计量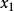 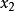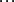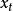， ， ， 可利用求极值的方法来满足上式的条件。为此，对残余误差的平方和 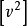求导数，并令其为零，有

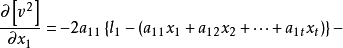
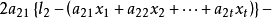
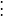
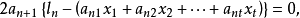用高斯符号表示有

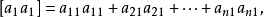
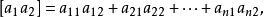
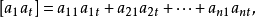
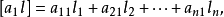则可得

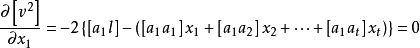同理有

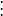
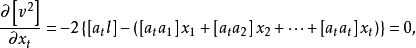注意到上式中各二阶偏导数恒正，即

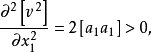
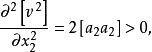
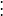
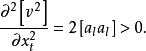
由此可知，上面各方程求得的极值是最小值，满足最小二乘条件，因而也是所要求的估计量，最后把它写成

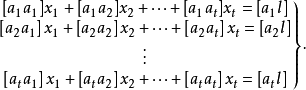
上式即为等精度测量的线性参数最小二乘法处理的正规方程。这是一个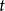 元线性方程组，当其系数行列式不为零时，有唯一确定的解，由此可解得欲求的估计量。1