[科普中国]-一般位置直线

定义

在三投影面体系中，与三个投影面都倾斜的直线称为一般位置直线(图1)。一般位置直线段的投影规律是：三个投影均为缩短了的直线段。三个投影均不反映直线段与投影面夹角的实际大小。2

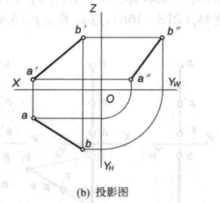
一般位置直线投影特性一般位置直线的投影特性（如图2、3）：

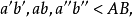各投影与投影轴倾斜且不能反映AB与各投影面的夹角。3

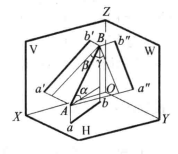
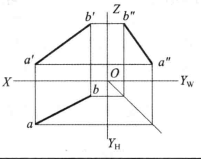
倾角与实长的求法用图解法求实长和倾角从一般位置直线投影特性可知，直线AB的三个投影均小于AB，不能反映直线AB的实长及它们对各投影面的倾角，但我们可用图解法来求出其实长和倾角，具体作法如图4所示。3

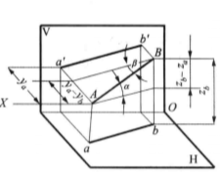
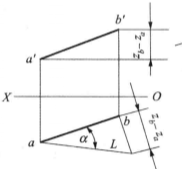
在图4 （a）中，平行四边形ABba垂直于H面，如过点A在此平面内作一直线平行于ab，则在此平面内形成一直角三角形，其斜边即为此直角三角形的实长AB，直角底边平行且等于ab，而其另一直角边则为A和B两点的Z坐标差。如在投影图上已知直线AB的水平投影ab以及直线AB两点的Z坐标差（此差可在正面投影中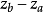量得），则可以通过作一直角三角形而求出实长L及α角。α是直线AB与它在H面上的正投影间的夹角。因此，必是直线AB与H面的夹角，如图4(b)所示。这就是通常所说的用直角三角形法求直线的实长与倾角的方法，也是利用投影来图解空间几何问题度量的一个例子。

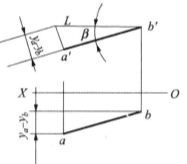
同理，如图4（c）所示，可求出直线AB的实长L及其与V面的夹角β。在子面体系中，还可利用点A和点B的Z坐标差作一直角三角形，而求出直线AB的实长L及其与W面的倾角γ。3

用直角三角形法求其L、α、β、γ的规律(1)以直线AB的水平投影ab为直角底边，以点A和点B的Z坐标差为直角边所组成的直角三角形，其斜边即为AB的实长L，L与ab的夹角即为AB与H面的夹角α。

(2)以直线AB的正面投影a'b’为直角底边，以点A和点B的Y坐标差为直角边所组成的直角三角形，其斜边即为AB的实长L，L与a'b’的夹角即为AB与V面的夹角β。

(3)以直线AB的侧面投影a''b''为直角底边，以点A和点B的X坐标差为直角边所组成的直角三角形，其斜边即为AB的实长L，L与a''b''的夹角即为AB与W面的夹角γ。3