简介
递归可枚举集合(英语:Recursively enumerable set)是可计算性理论或更狭义的递归论中的一个概念。可数集合S被称为是递归可枚举、计算可枚举的、半可判定的或可证明的,如果
存在一个算法,只有当输入是S中的元素时,算法才会中止。
或者等价的说,
存在一个算法,可以将S中的成员枚举出来。也就是说该算法的输出就是S的成员列表:s1,s2,s3, ... 如果需要它可以永远运行下去。
包含所有可递归枚举集合的复杂性类是RE。
共同的编程意义会暗示出如何转换一种算法到等价的另一种算法。第一种情况说明了为什么有时说半可判定的,而第二种情况说明了为什么叫计算可枚举的。
定义可数集合 是递归可枚举的,如果存在一个偏可计算函数
是递归可枚举的,如果存在一个偏可计算函数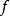 使得
使得
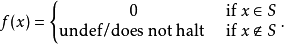 换句话说,
换句话说,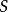 是
是 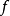 的域:
的域:
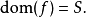 (注意这是偏函数的域的两种可能意义之一,是在递归论中所偏好的定义域。参见在偏函数中的讨论。)集合
(注意这是偏函数的域的两种可能意义之一,是在递归论中所偏好的定义域。参见在偏函数中的讨论。)集合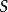 被成为co-递归可枚举的或co-r.e.,如果
被成为co-递归可枚举的或co-r.e.,如果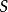 的补集是递归可枚举的。
的补集是递归可枚举的。
等价定义 可数集合
可数集合 被叫做递归可枚举的,如果存在着一个偏可计算函数,使得
被叫做递归可枚举的,如果存在着一个偏可计算函数,使得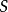 是
是 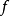 的值域:
的值域:
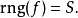
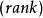
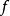 被称为枚举函数,因为它关联上一个枚举上的次序到
被称为枚举函数,因为它关联上一个枚举上的次序到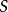 的每个元素1。
的每个元素1。
详细解释设有一集合A与一函数α(x),如果α(x)=0当且仅当x∈A,则α(x)叫做A的特征部分函数,如果还有α(x)=1,当且仅当x∈A,则α(x)叫做A的特征全函数,简称特征函数。如果一集合A的特征部分函数(也是特征函数)是递归全函数,则A叫做递归集;如果一集A的特征部分函数是递归部分函数,则A叫做部分递归集;部分递归集又可定义为某个递归部分函数的定义域。显然,A为递归集当且仅当:任给x,x属于A与否,恒可在有限步内判定;A为部分递归集当且仅当:任给x,如果x∈A,则必可在有限步内判定,但如果x不属于A,可能永远不知道这件事(除非从别的途径)。因此有下列结果:
①如果A为递归集,则A为部分递归集;
②A为递归集当且仅当A的补集亦为递归集;
③A为递归集当且仅当A与它的补集都是部分递归集。
最后一点可看出:如果x∈A,因A为部分递归集必可在有限步内看出;如果x唘A,因A的补集为部分递归集亦可在有限步内看出,从而A必为递归集。
递归可枚举集是指它是某个一般递归函数(即递归全函数)ƒ(x)的值域。因为递归全函数ƒ(x)的每一个值都可在有限步内算出,可以逐步地计算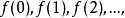 从而得出递归可枚举集的所有元素。这便是递归可枚举集名称的来源。ƒ(x)叫做该集的枚举函数,可能有两值ƒ(α)与ƒ(b)是相等的,即容许重复枚举。如果ƒ(x)是不减函数或(严格)递增函数,便叫做不减枚举或(严格)递增枚举。
从而得出递归可枚举集的所有元素。这便是递归可枚举集名称的来源。ƒ(x)叫做该集的枚举函数,可能有两值ƒ(α)与ƒ(b)是相等的,即容许重复枚举。如果ƒ(x)是不减函数或(严格)递增函数,便叫做不减枚举或(严格)递增枚举。
显然,如果x在一个递归可枚举集A内,必可在有限步内判定(只须依次计算ƒ(0),ƒ(1),…,便可);但如果x不在A内,而A又不是严格递增枚举,则很可能人们永远也不知道这事。根据上述部分递归集的特性,可知递归可枚举集都是部分递归集。反之,如果A为部分递归集,命其特征部分函数为α(x),当A为空集时,它当然不是任何递归全函数的值域,当A非空集时,则在第一阶段对α(0),α(1)各计算1步,第二阶段对α(0),α(1),α(2)各计算2步,…,第n阶段对α(0),α(1),α(2),…,α(n)各计算n步,…,并把首先出现的α(x)=0的根取为ƒ(0),以后在每一阶段之末均把在该阶段时所已知的α(x)=0的根取为ƒ在新主目处的值,ƒ必为递归全函数,而且A的元素恰巧便是ƒ(0),ƒ(1),…的值。可见非空的部分递归集必是递归可枚举集。一般还把空集也算作递归可枚举集,这样两种集便一致起来了。
可以证明,A为递归可枚举集当且仅当它是某个原始递归函数的值域,又当且仅当它是某个初等函数的值域。另一方面,A为递归可枚举当且仅当它是某个递归部分函数的值域,只须仿照上法,在第n阶段计算ƒ(0),ƒ(1),…,ƒ(n)各n步,便可把递归部分函数的值全部都枚举出来了。
已有办法把全体递归部分函数全部枚举起来,因此也可以把它们的定义域或值域全部枚举起来。设把第 x个递归部分函数的定义域(值域)记为Wx,则Wx便是全体部分递归集(递归可枚举集)的枚举(注意其中是有重复的)。如命K={x:x∈Wx}(即如果x恰巧在第x个部分递归集之内,便把x作为K 的元素),则K是一个递归可枚举集但不是递归集,从而K 的补集既不是递归集又不是递归可枚举集。这是人们作出的第一个不是递归可枚举集的例子,它也是一个很重要的集,对它已有充分的研究。
此外,如果ƒ 为递归部分函数,A为递归可枚举,则ƒ-1(A)也是递归可枚举集。 著名的希尔伯特第10问题是:有没有一个能行方法,可决定任给的一个不定方程是否有整数解?这里P、Q是两个具有整系数的多项式。这个问题到1970年已经被否定地解决了,即如果把“能行方法”理解为“用计算递归全函数的方法”,那末可以证明:这个能行方法是没有的。因为任何一个部分递归集(递归可枚举集)A,都有两个带整系数的多项式P、Q,使得 特别是当A即集合K时,也可找出相应的两个多项式P、Q。既然K不是递归的,x属于K与否是不能递归地判定的,那末对于“什么样的x能够使有解”的问题,也就不能递归地判定了。 上面关于集合的讨论可以推广到n元关系去。就n元关系R(x1,x2,…,xn)而言,如果R(x1,x2,…,xn)成立当且仅当,则ƒ(x1,x2,…,xn)叫做R(x1,x2,…,xn) 的特征部分函数,如果还要求:R(x1,x2,…,xn)不成立当且仅当,则ƒ 叫做R的特征全函数,简称特征函数。如果关系R(x1,x2,…,xn)的特征部分函数(也是特征函数)是一个递归全函数,则R叫做递归关系;如果R(x1,x2,…,xn)的特征部分函数是递归部分函数,则R叫做部分递归关系。有了这些定义以后,以上的讨论完全可以推广到递归关系与部分递归关系方面来。当然,由于函数的值是一个数而不是n元向量,所以“递归可枚举关系”不能定义为某个递归全函数的值域而只能定义为部分递归关系。 但是对递归关系而论,有下列的结果,这是讨论递归时所没有的。
① R(x1,x2,…,xn)为部分递归关系当且仅当有一个n+1元递归关系或部分递归关系 W 使得。
② R(x1,x2,…,xn)为部分递归关系当且仅当有一个n+m 元递归或部分递归关系W 使得。
③ A为部分递归集当且仅当有一个二元递归或部分递归关系W 使得2。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国