基本介绍
考虑线性时变系统:
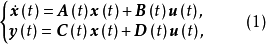
其中,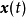 为n维状态向量,
为n维状态向量,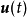 为p维输人向量,
为p维输人向量,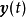 为q维输出向量。
为q维输出向量。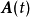 、
、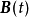 、
、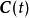 和
和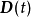 分别为
分别为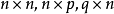 和
和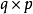 时变矩阵。
时变矩阵。
定义1 对于线性时变系统(1),根据系统矩阵构造如下形式的时变系统:
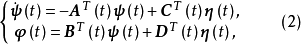 其中,
其中,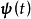 为n维状态向量,
为n维状态向量,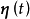 为q维输入向量。
为q维输入向量。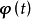 为p维输出向量。称系统(2)为系统(1)的对偶系统。2
为p维输出向量。称系统(2)为系统(1)的对偶系统。2
原系统与其对偶系统之间的属性下面介绍原线性系统与其对偶系统之间具有的属性。
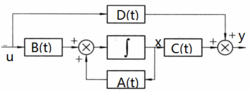
系统结构图的对偶性对偶系统的结构图如图1所示。从图中可看出,互为对偶的系统在结构上,如信号流向、状态、输入和输出的作用点、求和点位置等呈现对偶属性。如果称结构图左部的量为“输入量”,结构图右部的量为“输出量”,则图(a)表示用“输入量”控制“输出量”,是一个控制问题;图(b)表示用“输出量”求得“输入量”,是一个估计问题。因此,对偶性原理揭示了最优控制和最优估计之间的内在联系。2
对偶系统的线性属性和时变属性若原系统(1)为线性系统,则其对偶系统(2)也为线性系统;若原系统(1)为时变(或定常)系统,则其对偶系统(2)也为时变(或定常)系统。2
状态转移矩阵的对偶性原线性系统(1)的状态转移矩阵为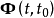 ,其对偶系统(2)的状态转移矩阵为
,其对偶系统(2)的状态转移矩阵为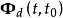 ,则由状态转移矩阵的性质可知,两者之间存在如下的关系:
,则由状态转移矩阵的性质可知,两者之间存在如下的关系:
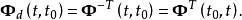
时序的对偶性若原线性系统(1)的运动是状态点在状态空间中,由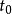 至
至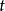 正时向转移,则其对偶系统(2)的运动是状态点在状态空间中,由
正时向转移,则其对偶系统(2)的运动是状态点在状态空间中,由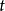 至
至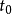 反时向转移。2
反时向转移。2
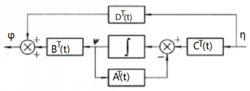
参数矩阵的对偶性若记原线性系统与其对偶系统分别为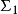 和
和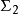 ,则原线性系统
,则原线性系统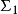 与其对偶系统
与其对偶系统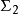 的参数矩阵之间具有如下对应关系:
的参数矩阵之间具有如下对应关系:
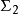 系统矩阵=一
系统矩阵=一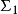 系统矩阵的转置,
系统矩阵的转置,
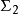 输入矩阵=
输入矩阵=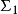 输出矩阵的转置,
输出矩阵的转置,
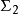 输出矩阵=
输出矩阵=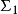 输入矩阵的转置。2
输入矩阵的转置。2
对偶系统的性质若系统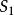 和系统
和系统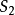 互为对偶,且系统
互为对偶,且系统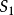 的传递函数矩阵为
的传递函数矩阵为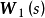 ,系统
,系统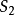 的传递函数矩阵为
的传递函数矩阵为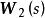 ,则有
,则有
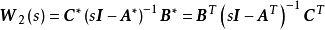
 也就是说,互为对偶的系统其传递函数阵是互为转置的。
也就是说,互为对偶的系统其传递函数阵是互为转置的。
由于
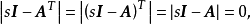 所以还可以看出,互为对偶的系统其特征方程是相同的。3
所以还可以看出,互为对偶的系统其特征方程是相同的。3




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国