定义
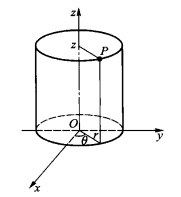
在空间直角坐标系中,任给一点P,设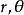 是点
是点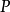 在
在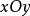 面上投影点的极坐标,
面上投影点的极坐标,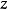 是点
是点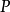 的竖坐标,则称
的竖坐标,则称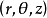 是点
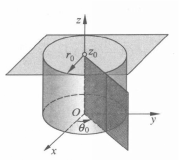
是点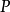 的柱面坐标(见图1),记为
的柱面坐标(见图1),记为 ,其中
,其中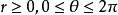 (或
(或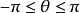 ),
),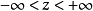 。1
。1
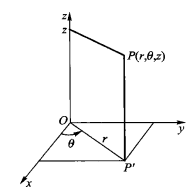
求曲面的柱面坐标方程的方法求曲面的柱面坐标方程的方法与步骤,和求直角坐标方程类似,就是把曲面看作适合某种条件的点的集合或轨迹,将已知条件用曲面上点的柱面坐标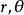 和
和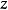 的关系式表示出来,就得到曲面的柱面坐标方程
的关系式表示出来,就得到曲面的柱面坐标方程 。1
。1
柱坐标的坐标面特别地,方程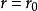 表示以
表示以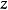 为轴的圆柱面;
为轴的圆柱面;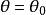 表示过
表示过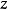 轴的半平面;
轴的半平面;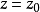 表示垂直于
表示垂直于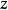 轴的平面,这三组面两两垂直,称为柱面坐标的坐标面,坐标面的交线称为坐标线。从图2可知,空间每一点P总可看作位于某一母线平行于z轴的圆柱面上,并有三条坐标线(过P垂直于z轴的射线、平行于z轴的直线和圆心在z轴且与z轴垂直的圆周)通过,所以把
轴的平面,这三组面两两垂直,称为柱面坐标的坐标面,坐标面的交线称为坐标线。从图2可知,空间每一点P总可看作位于某一母线平行于z轴的圆柱面上,并有三条坐标线(过P垂直于z轴的射线、平行于z轴的直线和圆心在z轴且与z轴垂直的圆周)通过,所以把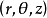 称为点P的柱面坐标由此而来。1
称为点P的柱面坐标由此而来。1
当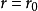 (常数)时,坐标面为柱面;
(常数)时,坐标面为柱面;
当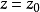 (常数)时,坐标面为平面;
(常数)时,坐标面为平面;
当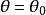 (常数)时,坐标面为半平面(见图3).2
(常数)时,坐标面为半平面(见图3).2
柱面坐标变换空间中的任意点P的位置由3个参数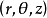 给出,其意义如图2所示,
给出,其意义如图2所示,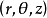 称为柱面坐标。
称为柱面坐标。
从其与空间直角坐标系的关系得变换如下,此变换称为柱坐标变换。2
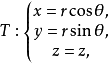 其中
其中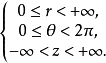
柱坐标的体积微元柱坐标的体积微元由6个坐标面围成。
(1)半平面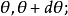
(2)圆柱面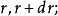
(3)平面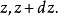
由于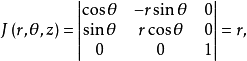 所以
所以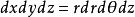 见图(4)。2
见图(4)。2
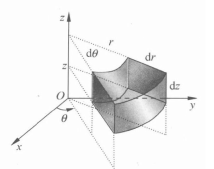
柱坐标的换元公式如果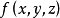 在V上连续,在变换
在V上连续,在变换
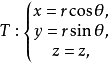 其中
其中
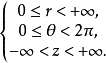 下,有
下,有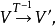 则
则
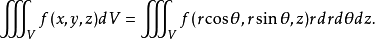 值得注意的是,当r=0时,上面的公式亦成立.
值得注意的是,当r=0时,上面的公式亦成立.
在计算中,通常找出V在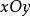 的投影区域D,即
的投影区域D,即
 从而得
从而得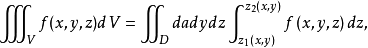 ,然后在二重积分中利用极坐标变换即可.2
,然后在二重积分中利用极坐标变换即可.2
化曲面的普通方程化为柱面坐标方程设P点的柱面坐标为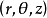 ,点
,点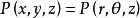 满足
满足
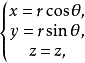 或
或 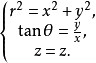
利用上述公式,可以化曲面的普通方程化为柱面坐标方程:
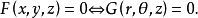
一般来说,如果一个曲面以z轴为对称轴,并且普通方程中含有 那么使用柱面坐标方程表示该曲面,可能会更简单。
那么使用柱面坐标方程表示该曲面,可能会更简单。
例如,半球面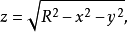 旋转抛物面
旋转抛物面 锥面
锥面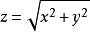 化为柱坐标方程分别为
化为柱坐标方程分别为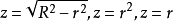 。而椭球面
。而椭球面 的柱面方程为
的柱面方程为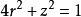 。1
。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国