公元前3世纪下半叶古希腊科学家阿基米德在论著《群牛问题》中记载了本问题。该问题在1880年由阿姆托尔提供了一种解答,该解答需要求解二元二次方程t2-d*u2=1,因d的值达400多万亿,所以完全问题的最小解中牛的总数是一个超过20万位的数,可见阿基米德当时未必解出过这个问题,且它的结果也与实际不符。历史上对这个问题的研究丰富了初等数论的内容。
问题的来历公元前3世纪下半叶古希腊科学家阿基米德在论著《群牛问题》中记载了本问题。原文用诗句写成:
朋友,如果你自认为还有几分聪明,
请来准确无误地算一算太阳神的牛群,
它们聚集在西西里岛,
分成四群悠闲地品尝青草。
第一群象乳汁一般白洁,
第二群闪耀着乌黑的光泽。
第三群棕黄,
第四群毛色花俏,
每群牛有公有母、有多有少。
先告诉你各群的公牛比例:
白牛数等于棕牛数再加上黑牛数的三分之一又二分之一。
此外,黑牛数为花牛数的四分之一加五分之一,再加上全部棕公牛。
朋友,你还必须牢记花牛数是白牛的六分之一又七分之一,
再搭上全部的棕色公牛。
但是,各群的母牛都有不同的比例:
白色的母牛数等于全部黑色公母牛的三分之一又四分之一。
而黑母牛又是全部花牛的四分之一加上五分之一,
请注意,母牛公牛都要算进去。
同样的,花母牛的数字是全部棕牛的五分之一加六分之一。
最后,棕色母牛与全部白牛的六分之一加七分之一相一致。
朋友,若你能确切地告诉我这些公牛母牛膘肥体壮、毛色各异,
一共有多少聚集在那里,
你就不愧为精通算计。
但你还称不上聪明无比,
除非你能回答如下的问题:
把所有的黑白公牛齐集一起,
恰排成正方形,整整齐齐。
辽阔的西西里岛草地,
还有不少公牛在聚集。
当棕色的公牛与花公牛走到一起,
排成一个三角形状。
棕色公牛、花公牛头头在场,
其他的牛没有一头敢往里闯。
朋友,你若能够根据上述条件,
准确说出各种牛的数量,
那你就是胜利者,
你的声誉将如日月永放光芒。
题目: 西西里岛的草地上, 太阳神的牛群中有公牛也有母牛,公牛母牛都是白、 黑、 花、 棕4种毛色; 白色公牛多于棕色公牛, 多出的头数是黑色公牛的 12+13 ; 黑色公牛多于棕色公牛, 多出的头数是花公牛的 14+15 ; 花公牛多于棕色公牛, 多出的头数是白色公牛的 16+17 ; 白色母牛是黑牛的 13+14 ; 黑色母牛是花牛的 14+15 ;花母牛是棕色牛的 15+16 ; 棕色母牛是白色牛的 16+17 .问各色公牛与母牛有多少头?
问题的深意阿基米德的论文向来是以命题的形式来表达的,而这篇的体例不同,它是用诗句写成的。标题是给埃拉托塞尼的信。胡尔奇(Hultsch)曾猜想这是阿基米德“显本领(tour de force)”之作,以此向亚历山大的学者们(特别是阿波罗尼奥斯)挑战。但它的真实性颇值得怀疑,因为“群牛问题”大概很早以前就已存在,阿基米德只是重新研究而已,诗句也未必出自他的手1。
问题的叙述诗的大意是:西西里岛草原上有一大群牛,公牛和母牛各有4种颜色。设W、X、Y、Z分别表示白、黑、黄、花色的公牛数, w、x、y、z分别表示这白、黑、黄、花色的母牛数。
要求有
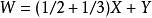 ,
,
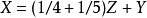 ,
,
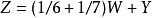 ,
,
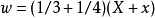 ,
,
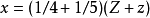 ,
,
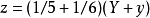 ,
,
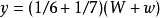 ,
,
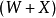 为一个正方形(数),
为一个正方形(数),
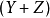 为一个三角形(数)(即形如
为一个三角形(数)(即形如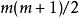 的数,m为正整数)。
的数,m为正整数)。
求各种颜色牛的数目。
倒数第二个条件中的正方形数有两种解释:
一种是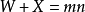 ,因为要挤成一个正方形,还需要考虑身长与体宽的比,故右端不是任意两个正整数之积mn而是
,因为要挤成一个正方形,还需要考虑身长与体宽的比,故右端不是任意两个正整数之积mn而是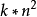 (k是常数),称为“较简问题”。
(k是常数),称为“较简问题”。
另一种为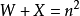 (完全平方数),即长与宽上牛的数目相等,称为“完全问题”2。
(完全平方数),即长与宽上牛的数目相等,称为“完全问题”2。
问题的解决“较简问题”已由武尔姆解决。“完全问题”在1880年为阿姆托尔(Amthor)所解决。
即使较简问题,牛的总数也已达到头之多!
而完全需要求解二元二次方程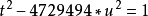 。
。
最小解牛的总数是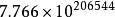 ,位数超过20万!当时阿基米德未必解得出来。
,位数超过20万!当时阿基米德未必解得出来。
而即使没有最后两个条件,群牛问题的最小正数解也达50'389'082,故它的叙述自然与实际不符——西西里岛再大也装不下这么多牛的。但历史上对这个问题的研究丰富了初等数论的内容3。
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国