简介
对一个元素在域F中的矩阵,有:
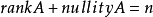 同样的,对于一个从 F线性空间V射到 F线性空间W的线性变换T:T: V→ W, T的秩是它的象的维度,T的零化度是它的核(零空间)的维度。我们有:
同样的,对于一个从 F线性空间V射到 F线性空间W的线性变换T:T: V→ W, T的秩是它的象的维度,T的零化度是它的核(零空间)的维度。我们有:
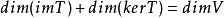 也就是:
也就是: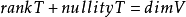 实际上定理在更广的范围内也成立,因为V和 F可以是无限维的。
实际上定理在更广的范围内也成立,因为V和 F可以是无限维的。
证明
证明的方法基于线性空间的基和同构。
设 V是一个有限维线性空间,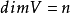 ,对一个从V射到 F的线性变换 T,ker T是 V的一个子空间。设 是 ker T的一组基( p≤ n)。根据基扩充定理,可以被扩充为 V的一组基:。 是一组线性无关的向量,设 H是它们张成的子空间,那么 V是 ker T与 H的直和:
,对一个从V射到 F的线性变换 T,ker T是 V的一个子空间。设 是 ker T的一组基( p≤ n)。根据基扩充定理,可以被扩充为 V的一组基:。 是一组线性无关的向量,设 H是它们张成的子空间,那么 V是 ker T与 H的直和:
所以,按照直和的性质,有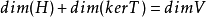 ,并且,同时,,其中。考虑T限制在 H上到 im T的线性变换:
,并且,同时,,其中。考虑T限制在 H上到 im T的线性变换:
下证是一个双射:
是一个单射,因为, 。 是一个满射,因为, ,而且 ,其中。 于是 ,其中,所以是一个满射。 于是是一个H到 im T的同构,所以
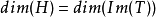 综上所述,即有:
综上所述,即有: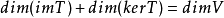 也就是:
也就是: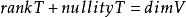
证明[编辑]证明的方法基于线性空间的基和同构。
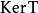 设
设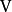 是一个有限维线性空间,其维度
是一个有限维线性空间,其维度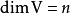 。对一个从
。对一个从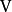 射到
射到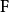 的线性变换
的线性变换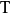 ,它的核是
,它的核是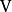 的一个子空间。设
的一个子空间。设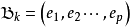 是
是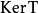 的一组基
的一组基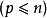 。根据基扩充定理,
。根据基扩充定理,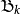 可以被扩充为
可以被扩充为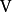 的一组基:
的一组基: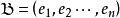 。除了
。除了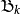 的
的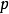 个向量以外,另外的
个向量以外,另外的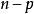 个向量
个向量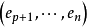 是一组线性无关的向量。设是它们张成的子空间,那么
是一组线性无关的向量。设是它们张成的子空间,那么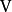 是子空间
是子空间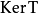 与
与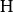 的直和1:
的直和1:
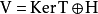
所以,按照直和的性质,有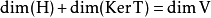 ,并且这两个子空间的交集为
,并且这两个子空间的交集为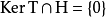 。同时,
。同时,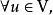 都可以写成
都可以写成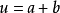 的形式,其中
的形式,其中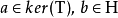 。考虑
。考虑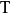 限制在
限制在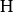 上到
上到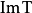 的线性变换
的线性变换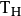 :
:
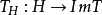
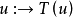
下证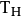 是一个同构。首先由于
是一个同构。首先由于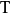 是线性映射,所以
是线性映射,所以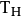 是线性映射。只需证明它也是双射:
是线性映射。只需证明它也是双射:
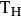 是一个单射,因为
是一个单射,因为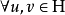
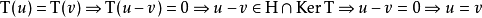 ,。
,。
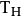 是一个满射,因为
是一个满射,因为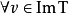 ,
,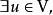 ,使得
,使得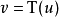 ,而且
,而且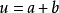 ,其中
,其中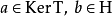 。 于是
。 于是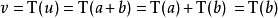 ,其中
,其中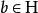 ,所以
,所以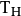 是一个满射。
是一个满射。
既然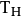 是一个
是一个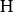 到
到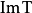 的同构,那么
的同构,那么
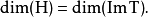 综上所述,即有:
综上所述,即有:
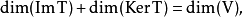 也就是:
也就是:

其他表达形式及推广正合列
秩-零化度定理是抽象代数中的同态基本定理在线性空间上的表现形式。如果用更现代的语言,定理可以表示为:如果
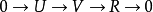 是线性空间中的一个短正合列,那么有:
是线性空间中的一个短正合列,那么有: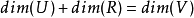 其中 R表示 im T, U表示 ker T。 在有限维的情况下,上式可以作进一步推广。如果
其中 R表示 im T, U表示 ker T。 在有限维的情况下,上式可以作进一步推广。如果
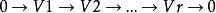 是有限维线性空间中的一个正合列,那么有: 在有限维线性空间中,秩-零化度定理还可以用线性变换的指标(index)描述。线性变换的指标指的是,对于线性变换
是有限维线性空间中的一个正合列,那么有: 在有限维线性空间中,秩-零化度定理还可以用线性变换的指标(index)描述。线性变换的指标指的是,对于线性变换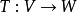 :
:
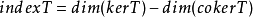 其中
其中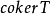 表示 T的余核。正如 ker T表示方程
表示 T的余核。正如 ker T表示方程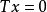 线性无关的解的“个数”,
线性无关的解的“个数”,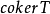 表示使得方程
表示使得方程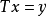 有解而必须加于 y的限制条件的个数。
有解而必须加于 y的限制条件的个数。
这时秩-零化度定理表述为: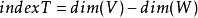 可以看到,在这种表述下,我们可以很容易地得到 T的指标,而不必对 T作深入研究。更深入的结果可以参见Atiyah–Singer指标定理(en:Atiyah-Singer index theorem)。Atiyah–Singer指标定理说明某些微分算子的指标可以通过涉及的空间的几何性质得到2。
可以看到,在这种表述下,我们可以很容易地得到 T的指标,而不必对 T作深入研究。更深入的结果可以参见Atiyah–Singer指标定理(en:Atiyah-Singer index theorem)。Atiyah–Singer指标定理说明某些微分算子的指标可以通过涉及的空间的几何性质得到2。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国