[科普中国]-积分第二中值定理

定义

设f(x)在[a,b]上可积，g(x)在[a,b]上单调，则存在ξ∈[a,b]，使得

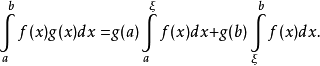
特别地1，若对于任意x∈[a,b]有g(x)=1,则原公式可化为：存在[a,b]上的点ξ使

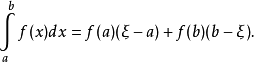
(注：实际上，定理结论中的 ξ∈[a,b] 可以加强到 ξ∈(a,b)，不过证明方法需要作适当修正)

推导这个定理的推导比较复杂，牵扯到积分上限函数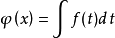： 。以下用 表示从a到b的定积分。

首先需要证明，若函数f(x)在[a,b]内可积分，则Φ(x)在此区间内为一连续函数。

证明：设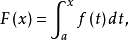 则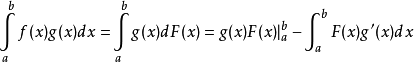

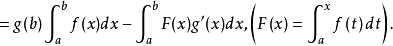
因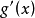 在[a,b]上不变号，则由积分第一中值定理知，在[a,b]上至少存在一点ξ，使得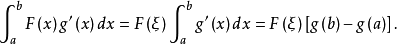

于是，有

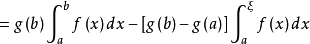
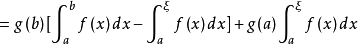
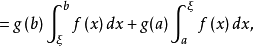
即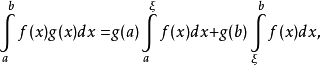得证。

应用在一些比较复杂的极限证明过程中应用积分第二中值定理可以得到很好的结果，而且计算过程简单易懂，证明方式也很多，下面给出它在各个方面的重要应用2。

1.定理的直接应用例1.设f(x)在[a,b]上可积,g(x)在[a,b]上单调递增且非负,在a,b处连续,那么在[a,b]上存在ξ,使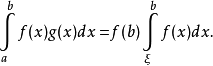

证 明 :令x=b-t,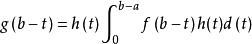 ,因为h(t)非负且单调递减( 0