[科普中国]-策略空间

定义定义一

在某一问题中，可以采取的策略的总体称为策略空间，每一个策略都是策略空间的一个点。

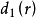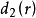策略空间是决策理论中的一个概念。举例来说，一个工厂生产一批数目很大的产品，我们采取抽样的办法从其中抽取n样，以此来做出接收或拒绝这批产品的决策。针对这一问题，可以采取多种决策方案。每一个决策方案就称为一个策略。符号r为抽取的n样产品中次品的件数，并且把接收记作“1”，把拒绝记作“0”，可以把策略规定为：次品件数过半就拒绝，否则就接收。还可规定为：次品件数大于2就拒绝，否则就接收。在数学上，这两个策略是两个函数，记作与。于是

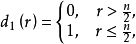
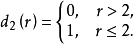
当然，还可以制定出更多的策略。这些可以采取的策略的总体就是一个策略的空间。

系统最优化工程的研究目的，就是要考察如何从策略空间中选取一个最优策略，使该系统达到某种意义上的最优化。3

定义二策略空间(Strategy Space)是指博弈各方可供选择的策略或行为的集合。比如，一个参与人的所有可选择的策略集合就是这个参与人的策略空间。

策略集合指参与者可能采取的所有行动方案的集合。策略集合必须有两个以上元素，否则，无所谓对策，只是独自决策。

若参与者有有限个具体的策略可供选择，则称其有一个有限策略集合。例如，在单一次“剪刀、石头、布”里，每一个玩家都有一个有限策略集合{剪刀，石头，布}。若有无限个具体的策略可供选择，则称其有一个无限策略集合。例如，有规范出价增额的拍卖会有一个无限策略集合{$10，$20，$30，……}。另外，在分蛋糕问题里则有一个连续的策略集合{在蛋糕的百分之零至百分之百间的任一处切分}。

Strategy直译应为战略。不过战略一词对大多数博弈来讲显然过于抽象和宽泛了。每一个策略都对应一个相应的结果。因此每个博弈方可选的策略数量越多，博弈就越复杂。4

案例分析案例1 在水产养殖质量安全政府规制与养殖户的博弈模型中，参与人有政府和养殖户。借鉴公共选择理论，假设政府是追逐自身利益的经济人，其目标是政治收益最大化，而政治收益由声誉和经济绩效组成，政府规制会获得政治声誉但是同时要支付规制成本，这种成本反过来会影响政府其他方面的经济绩效。这样，水产养殖产品市场中政府规制取决于其成本和收益的比较。如果规制收益大于规制成本，那么政府将进行规制；规制成本大于规制收益时，政府就有不进行规制的动机。同时，假设养殖户的目标为收益最大化或成本最小化，养殖户生产高质量还是低质量的水产养殖产品，取决于其从事水产养殖的经济收益情况。

政府在水产养殖产品市场的策略空间为“规制、不规制”。养殖户控制水产养殖生产过程的策略空间为“高质量、低质量”生产方式，不论选择何种策略，其目的都是自己收益的最大化．由于消费者没有办法识别水产养殖产品的高、低质量，那么高、低质量的水产养殖产品价格都为P，即表明低质量产品能以次充好混同于高质量产品，水产养殖产品的产量为Q，而高质量的水产养殖产品的生产成本为Ch，低质量水产养殖产品的生产成本为Cl；政府保证了水产养殖产品市场的安全就获得的声誉收益为R，政府对养殖户的规制成本为Ca；处罚为F；另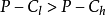，这保证了养殖户生产低质量水产养殖产品可以比生产高质量水产养殖产品获得超额利润，也就是说如果政府不进行规制，养殖户有生产低质量水产养殖产品的激励。这些信息为政府和养殖户的共同知识，因此，政府和养殖户之间的博弈是完全信息静态博弈。（更多分析请参考相应参考书籍）。5