定理
(空间向量分解定理) 如果三个向量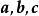 不共面,那么对空间任一向量p,存在一个惟一的有序实数组
不共面,那么对空间任一向量p,存在一个惟一的有序实数组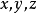 ,使1
,使1
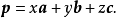
定理的证明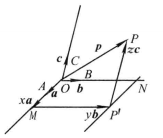
设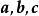 不共面(图1),过点O作
不共面(图1),过点O作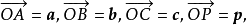 ,过点P作直线PP'平行于OC,交平面OAB于点P',在平面OAB内,过P'作直线
,过点P作直线PP'平行于OC,交平面OAB于点P',在平面OAB内,过P'作直线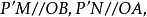 分别与直线OA,OB相交于点M,N,于是存在三个实数x,y,z,使
分别与直线OA,OB相交于点M,N,于是存在三个实数x,y,z,使
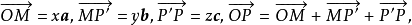 即
即
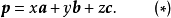 以下证明表达式(
以下证明表达式( )是惟一的:
)是惟一的:
令 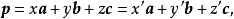
由于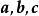 不共面,可推出
不共面,可推出
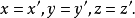
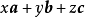 叫做向量
叫做向量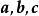 的线性表达式或线性组合。
的线性表达式或线性组合。
由上述定理可知,如果三个向量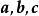 是不共面的向量(线性无关),那么
是不共面的向量(线性无关),那么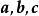 的线性组合
的线性组合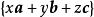 能生成所有的空间向量,这时
能生成所有的空间向量,这时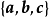 叫做空间的一个基****底,其中
叫做空间的一个基****底,其中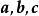 都叫做基向量。同时可知,空间任意三个不共面的向量都可构成空间的一个基底。
都叫做基向量。同时可知,空间任意三个不共面的向量都可构成空间的一个基底。
( )式叫做向量p的沿基向量的分解式。
)式叫做向量p的沿基向量的分解式。
如果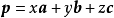 ,那么(x,y,z)叫做向量p关于
,那么(x,y,z)叫做向量p关于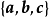 的坐标1。
的坐标1。
推论设O,A,B,C是不共面的四点,则对空间任一点P,都存在惟一的三个有序实数x,y,z,使
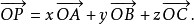
例题已知空间四边形OABC,M,N分别是对边OA,BC的中点,点G在MN上,且MG=2GN,试写出向量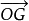 沿基底
沿基底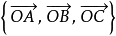 的分解式(图2)1。
的分解式(图2)1。
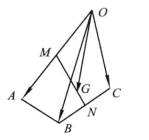
解: 由线段中点的向量表达式,得
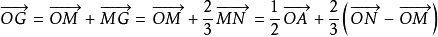
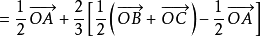
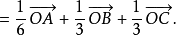




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国