[科普中国]-互相关

定义

两个函数f(x)和h(x)的互相关，由含参变量x的无穷积分定义，即

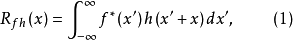或

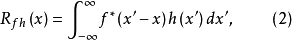类似于卷积，这里，参变量x和积分变量x′均为实数，函数f(x)和h(x)可以是实数，也可以是复数1。

(1)式表明，两个函数互相关的含义是：对两个函数分别作复数共轭和反向平移并使其相乘的无穷积分。(2)式表明，两个函数互相关的含义是，第一个函数依次作复共轭和平移后与第二个函数相乘的无穷积分。可以证明，两个定义式完全等价(可以互相导出)。从物理上看，互相关运算的结果反映了两个信号之间相似性的量度。特别是对于实函数f(x)和h(x)而言，其相关运算相当于求两函数的曲线相对平移 1个参变量x后形成的重叠部分与横轴所围区域的面积。

为了简化算式，通常特引入相关运算符号“⊗”，这样便可将f(x)和h(x)的互相关表示为1

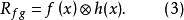
互相关的性质互相关有如下性质：

1) 互相关运算一般不服从交换律，即

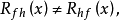但可以证明

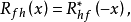并且，当函数f(x)和h(x)均为实数时，有

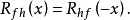
2) 互相关与卷积的意义不同，但互相关可以用卷积表示，即

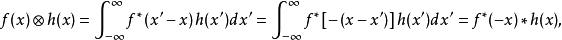显然，只有当函数h(x)为实的偶函数时，才有

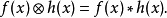由于相关与卷积的这种联系，相关运算的其他性质以及存在条件，可以利用其与卷积的关系，由卷积的相应性质导出。类似地，定义二维复函数f(x，y)和g(x，y)的互相关为

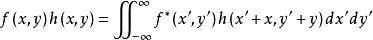
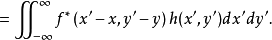同样，一维函数互相关的所有性质同样适用于二维函数的互相关，此处不再赘述1。