[科普中国]-脉冲函数

脉冲函数的定义

脉冲函数是英国物理学家狄拉克(Dirac)在20世纪20年代引人的，用于描述瞬间或空间几何点上的物理量。例如，瞬时的冲击力、脉冲电流或电压等急速变化的物理量，以及质点的质量分布、点电荷的电量分布等在空间或时间上高度集中的物理量。脉冲函数也称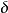函数。若在一维空间中，自变量为时间 t 的函数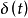，满足下述两个条件:

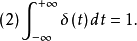
把满足上述两个条件的函数称为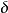函数，记作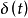。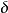函数是一种广义函数，也可以扩展到多维空间中，它的确切意义应该在积分运算下理解：其积分曲线高度为“无限高”，而宽度为“无限窄”，曲线下的面积等于1。因此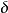，函数有下述关系式

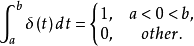
有了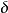函数的定义，就可以把处于x 轴上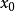点处、电量为q的点电荷，用线电荷密度函数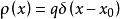来描述；把一维坐标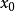点处的质点m，用质量线密度函数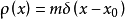来描述；......1。

δ函数的性质下面我们直接给出δ函数的几个基本性质2。

性质1 **(筛选性质)**设f(t)是定义在实数域上的有界函数，且在t0处连续，则

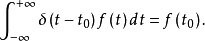特别地，当t0=0时，则有

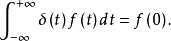
性质2 δ函数为偶函数，即。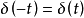

性质3 设u(t)为单位阶跃函数，即

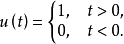则有

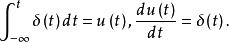
脉冲函数的傅氏变换根据δ函数的筛选性质，易知δ函数的傅氏变换为

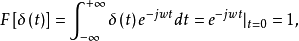即δ(t)与F(w)=1构成一傅氏变换对，按傅氏积分公式有

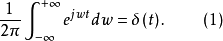这是一个关于δ函数的重要公式。

公式(1)并不是常规意义下的积分问题，故称δ(t)的傅氏变换为一种广义傅氏变换。在工程技术中，有许多函数并不满足绝对可积条件，如符号函数、单位阶跃函数以及正、余弦函数等，然而利用δ函数的傅氏变换就可以求出它们的傅氏变换了，从这个角度也可以看出引进δ函数的重要性2。