[科普中国]-相关图

定义

相关图(Scattor Diagram)又叫散布图，指把两个变量之间的相关关系，用直角坐标系表示的图表。在工业生产和科学研究中，经常遇到两个之间的关系问题： 一种是两个量之间是完全确定的函数关系；另一 种是两个量之间是不完全确定的对应关系。对于这种既相关又不完全确定的关系，就称为相关关系。人们应用画相关图，求出相关系数的方法来确定两个量之间的相关关系，就称为相关分析。 而当确定了相关关系之后，再用 统计检验与估计的方法对相关系数进行判断并求出回归方程的作法，称为回归分析1。

相关图的形式相关图的形式多种多样，可归纳为以下几种：

(1) 正强相关(x增大，y迅速 增大)，见图1；

(2)正弱相关(x增大，y缓慢增大)， 见图2；

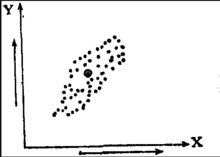
(3)负强相关(x增大，y迅速下降) ，见图3；

(4) 负弱相关(x增大，y缓慢下降)，见图4；

(5) 曲线相关(不成直线关系)，见图5；

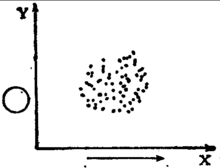
(6) 无相关(y不随x增减呈线性关系)，见图61。

函数关系与相关关系客观现象之间总是相互联系和相互依存的，现象之间的数量依存关系有两种不同的类型：一种是函数关系，另一种是相关关系。

当一个或几个变量取一定的值时，另一个变量有确定值与之相对应，我们称这种确定性的关系为函数关系。例如，某种商品的销售收人Y 与该商品的销售量X 以及该商品的价格P之间的关系可用Y=PX表示。

当一个或几个相互联系的变量取一定数值时，与之相对应的另一变量的值虽然不确定，但它仍按某种规律在一定范围内变化，变量间的这种具有不确定性的相互关系，称为相关关系。例如，劳动生产率与工资水平的关系、投资额与国民收人的关系、居民收人与消费支出的关系等都属于相关关系。商品需求量与该商品的价格、消费者的收入水平、消费者的偏好等的关系也属于相关关系2。

相关关系的种类按相关程度划分按客观现象间相关关系的密切程度不同可分为完全相关、不完全相关和不相****关三种类型。

当一种现象的数量变化完全由另一种现象的数量变化所确定时，称这两种现象间的关系为完全相关。因此也可以说函数关系是相关关系的一个特例。当两个现象彼此互不影响，其数量变化各自独立时，称为不相关。例如，经济发展水平与精神病患者的人数是不相关的。当两个现象之间的关系介于完全相关和不相关之间时，称其为不完全相关。一般说的相关现象都是指这种不完全相关关系。

按变量多少划分按所研究的变量多少，相关关系可分为单相关、复相关和偏相关。

我们把两个变量间的相关，即一个变量对另一个变量的相关关系，称为单相****关，单相关关系只有一个自变量。当所研究的是一个变量对两个或两个以上其他变量的相关关系时，称为复相****关。复相关关系有多个自变量。例如，某种商品的需求量与该商品价格以及消费者收人水平之间的相关关系便属于复相关。在某一现象与多种现象相关的场合，当假定其他变量不变时，其中两个变量的相关关系称为偏相关。如在上例中，若假定在消费者收入水平不变的条件下，商品需求量与其价格水平的关系就是偏相关关系。

按相关方向划分按相关关系的方向可分为正相关和负相关。

当两个变量的变化同方向时，这种同方向变动的关系称为正相关。例如，居民的消费支出随着居民收入水平的提高而提高。当两个变量的变化反方向时，这种反方向变动的关系称为负相关。例如，一定范围内，商品生产的规模越大，单位产品成本会越低。

按相关形式划分相关关系按相关的形式不同可分为线性相关和非线性相关。当两种相关现象之间的关系大致呈现为直线关系时，称之为线性相关或直线相关。例如，人均消费水平与人均收入水平之间通常呈线性关系。如果两种相关现象之间并不表现为直线的关系，而是近似于某种曲线方程的关系，则这种相关关系称为非线性相关或曲线相关。例如，某种产品的平均成本与产品总产量之间的关系就属于非线性相关关系2。