基本介绍
在数学中,有好些运算是互逆的。加和减,乘和除,乘方和开方,都属于这一类。一个自变数x,在经过一种运算之后得到y,再对这y进行相应的逆运算,结果是仍回到x。例如,以a乘x,得y =ax,将这y除以a,又得x,又如,将x平方,得 再对y开平方,又得x。今以
再对y开平方,又得x。今以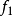 表示前一运算,以
表示前一运算,以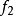 表示其逆运算,则上述关系可表示如下:
表示其逆运算,则上述关系可表示如下:
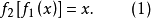 将
将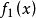 写在
写在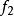 后的方括号内,就表示
后的方括号内,就表示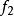 内的那个变数y当用
内的那个变数y当用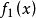 代入。例如,
代入。例如,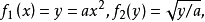 它们就符合上述条件,理由是:
它们就符合上述条件,理由是:
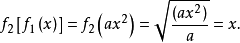 从
从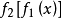 的组成上看,它也是一种复合函数。对式(1)两侧求导,当有:
的组成上看,它也是一种复合函数。对式(1)两侧求导,当有:
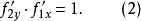 式中:
式中: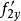 ——
——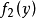 对y的导数;
对y的导数;
 ——
——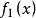 对x的导数;
对x的导数;
1——x对x的导数。
在式(1)中,一个运算是用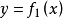 将x变成y,另一个运算是用
将x变成y,另一个运算是用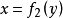 将y变成x,在这条件下,
将y变成x,在这条件下,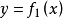 和
和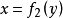 实际上是同一个方程,它们的图形也是同一条曲线。以
实际上是同一个方程,它们的图形也是同一条曲线。以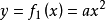 和
和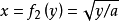 为例,将后一式平方,得
为例,将后一式平方,得 移除作乘,就得前一式。由此可见,若某个方程按对y求导要比对x求导方便,其切线的斜率y' (式(2)中的
移除作乘,就得前一式。由此可见,若某个方程按对y求导要比对x求导方便,其切线的斜率y' (式(2)中的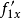 ) 也可用x' (式(2)中的
) 也可用x' (式(2)中的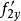 ) 的倒数表示;即:
) 的倒数表示;即:
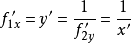 例如,所给的式子是
例如,所给的式子是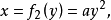 则
则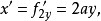 于是,
于是,
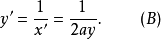 若将
若将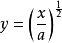 代人,
代人,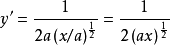 。而在将
。而在将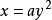 化为
化为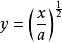 再求导时,
再求导时,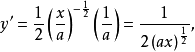 结果是相符的。但用式(B)来表示y',时常较为简捷。
结果是相符的。但用式(B)来表示y',时常较为简捷。
既然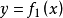 和
和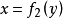 在图上是同一条线,那就容易混淆。又因
在图上是同一条线,那就容易混淆。又因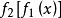 是表示将
是表示将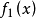 作为
作为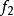 内的变数代人,至于
内的变数代人,至于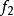 内的变数原先是用什么字母来代表,那却没有多大关系。因此,
内的变数原先是用什么字母来代表,那却没有多大关系。因此,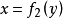 常改作
常改作 这也就是将原给的
这也就是将原给的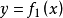 内的x和y对换,而后变形为
内的x和y对换,而后变形为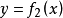 。这样的
。这样的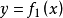 和
和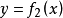 就叫互反函数2。
就叫互反函数2。
幂函数的反函数利用互反函数的这一对称性质来看幂函数,将见:
(1) 每一个幂函数的反函数仍是一个幂函数,因此,幂函数组成一个自反的函数族。这就是说,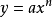 的反函数是
的反函数是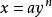 (且后式也可写作
(且后式也可写作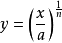 ),而它们都是幂函数。
),而它们都是幂函数。
(2)指数是真分数的幂函数,它的反函数(也是幂函的指数就大于1(是原来那个真分数的倒数)。由于指数大于1的幂函数的描点制图较易进行,可以先将反函数图形作出,再利用原函数和反函数对直线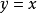 的对称,原函数作出2。
的对称,原函数作出2。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国