定义
就每一品种的晶体来说,必可觅得一套称为晶轴系的坐标轴系,从而使晶体上每个晶面在这三个晶轴上的倒易截数成简单的互质整数之比,即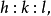 这一规律性称为有理指数定律,整数
这一规律性称为有理指数定律,整数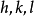 称为晶面的指数,符号
称为晶面的指数,符号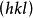 称为晶面的记号,有理指数定律突出地反映了晶体的点阵式构造。
称为晶面的记号,有理指数定律突出地反映了晶体的点阵式构造。
详细分析设晶体的晶胞系由向量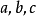 所规定,现以点阵点O为原点,向量
所规定,现以点阵点O为原点,向量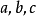 为三个坐标轴,而某一平面点阵的平面在三个坐标轴上的截点为
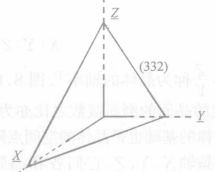
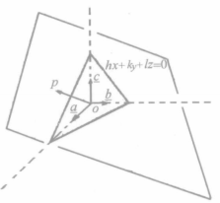
为三个坐标轴,而某一平面点阵的平面在三个坐标轴上的截点为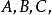 如图1中所示在图中,这个平面的截长为
如图1中所示在图中,这个平面的截长为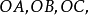 截数为
截数为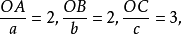 而倒易截数为
而倒易截数为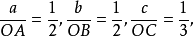 设在上述平面点阵中有一点阵点为P,并设
设在上述平面点阵中有一点阵点为P,并设
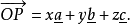
在此,P点的坐标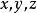 必为有理数,且应满足平面的方程:
必为有理数,且应满足平面的方程:
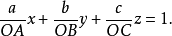 在上式中,平面上各点阵点的坐标
在上式中,平面上各点阵点的坐标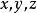 既为有理数,倒易截数
既为有理数,倒易截数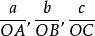 就不能不是有理数。这三个倒易截数既为有理数,它们之比必可通约为三个互质的整数之比,即
就不能不是有理数。这三个倒易截数既为有理数,它们之比必可通约为三个互质的整数之比,即 这样的三个互质整数可以代表上述平面点阵所属的平面点阵组,一般并用符号
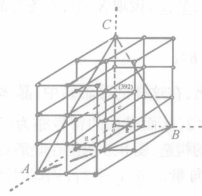
这样的三个互质整数可以代表上述平面点阵所属的平面点阵组,一般并用符号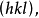 即(332)表示这一组平面点阵,图2 示出吐酒石晶体的点阵中若干平面点阵组的记号。
即(332)表示这一组平面点阵,图2 示出吐酒石晶体的点阵中若干平面点阵组的记号。
综上所述,我们就可以这样来选取晶轴系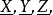 设取
设取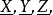 各与晶胞的
各与晶胞的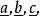 平行,并使
平行,并使
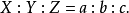 在此比率
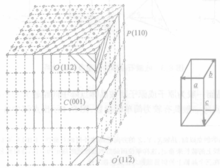
在此比率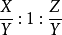 称为晶体的轴率中。图1示出,在这样的晶轴系中,晶体按平面点阵组(332)铺盖成的晶面的倒易截数之比亦为
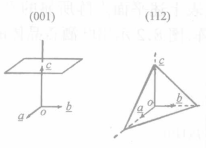
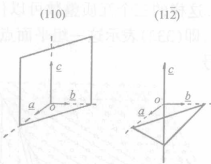
称为晶体的轴率中。图1示出,在这样的晶轴系中,晶体按平面点阵组(332)铺盖成的晶面的倒易截数之比亦为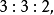 从而晶面的符号亦为(332),由此可见,有理指数定律的基础也是晶体的空间点阵式的构造。图3示出在吐酒石晶体的外形中安放的一套晶轴
从而晶面的符号亦为(332),由此可见,有理指数定律的基础也是晶体的空间点阵式的构造。图3示出在吐酒石晶体的外形中安放的一套晶轴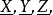 它们各和晶胞的向量
它们各和晶胞的向量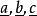 平行,而轴率为
平行,而轴率为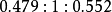 。
。
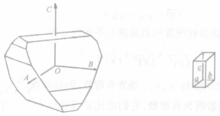
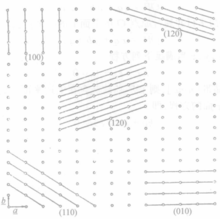
晶体上每个晶面一般为原子或原子团按晶体点阵中间距较大的平面点阵铺成的平面,而这样的平面点阵一般具有较为简单的指数,图4示出点阵中各平面点阵组的间距随其指数的增大而递减的情况。因此,晶体上各个晶面的指数一般限于简单的整数。
晶体点阵中的每一组直线点阵可用记号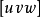 来表示,其中
来表示,其中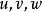 为三个互质的整数,记号为
为三个互质的整数,记号为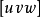 的直线点阵则与向量
的直线点阵则与向量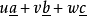 平行。例如
平行。例如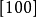 和
和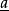 平行,
平行,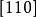 和
和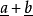 平行等。晶体上各个晶棱的记号和与其相应的直线点阵者同。在晶棱的记号
平行等。晶体上各个晶棱的记号和与其相应的直线点阵者同。在晶棱的记号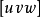 中,
中,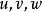 一般为简单的整数。
一般为简单的整数。
晶体上每一组与一通过晶体中心的假想直线平行的晶面形成一晶带,晶带中各对晶面间的交线亦必与上述假想直线平行,而后者一般称为带轴,晶带或带轴的记号与相应的晶棱者互相通用,若晶面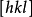 属于晶带
属于晶带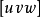 ,则
,则
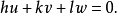 上述方程称为晶带方程,在晶体的晶轴系中,原点为O,晶轴为
上述方程称为晶带方程,在晶体的晶轴系中,原点为O,晶轴为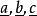 ,晶带
,晶带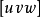 的带轴设为
的带轴设为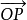 ,则
,则
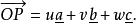 令P'为在与晶面
令P'为在与晶面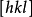 平行并通过原点O的平面上的一个任意点,则
平行并通过原点O的平面上的一个任意点,则
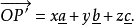 而式中P'点的坐标
而式中P'点的坐标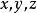 当满足下列方程
当满足下列方程
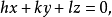 今晶面
今晶面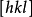 既属于晶带
既属于晶带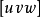 ,则OP必被包含在上述平面中,换言之,P点的坐标
,则OP必被包含在上述平面中,换言之,P点的坐标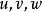 应满足上述平面的方程,即2
应满足上述平面的方程,即2





 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国