[科普中国]-高斯光束

简介

通常情形，激光谐振腔发出的基模辐射场，其横截面的振幅分布遵守高斯函数，故称高斯光束。1

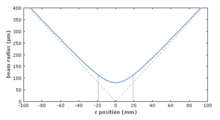
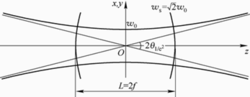
命名关于光斑大小的查询，其实问的就是光斑的束腰直径或束腰半径。束腰，是指高斯光绝对平行传输的地方。半径，是指在高斯光的横截面考察，以最大振幅处为原点，振幅下降到原点处的0.36788倍，也就是1/e倍的地方，由于高斯光关于原点对称，所以1/e的地方形成一个圆，该圆的半径，就是光斑在此横截面的半径；如果取束腰处的横截面来考察，此时的半径，即是束腰半径。沿着光斑前进，各处的半径的包络线是一个双曲面，该双曲面有渐近线。高斯光束的传输特性，是在远处沿传播方向成特定角度扩散，该角度即是光束的远场发散角，也就是一对渐近线的夹角，它与波长成正比，与其束腰半径成反比，故而，束腰半径越小，光斑发散越快；束腰半径越大，光斑发散越慢。

我们用感光片可以看到，在近距离时，准直器发出的光在一定范围内近似成平行光，距离稍远，光斑逐渐发散，亮点变弱变大；可是从光纤出来的光，很快就发散；这是因为，准直器的光斑直径大约有400微米，而光纤的光斑直径不到10微米。同时，对于准直器最大工作距离的定义，往往可理解为该准直器输出光斑的共焦参数，该参数与光斑束腰半径平方成正比，与波长成反比，计算式是：3.1415926*束腰半径*束腰半径/波长。所以要做成长工作距离（意味着在更长的传输距离里高斯光束仍近似成平行光）的准直器，必然要把光斑做大，透镜相应要加长加粗。

高斯光束基本特性振幅分布特性由高斯光束的表达式可以得到：

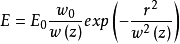
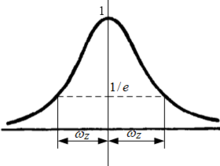
在z截面上，其振幅按照高斯函数规律变化，如图所示。将在光束截面内，振幅下降到最大值的1/e时，离光轴的距离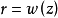定义为该处的光斑半径。

由w（z）的定义可以得到：

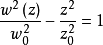
即光束半径随传输距离的变化规律为双曲线，在z=0时有最小值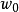，这个位置被称为高斯光束的束腰位置。2

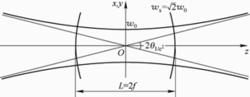
等相位面特性从高斯光束解的相位部分可以得到传输过程中的总相移为：

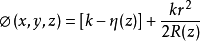
将上式同标准球面波的总相移表达式比较：

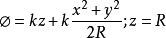
可以得出结论，在近轴条件下高斯光束的等相位面是以R(z)为半径的球面，球面的球心位置随着光束的传播不断变化，由R(z)的表达式可知：

z=0时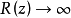，，此时的等相位面是平面；

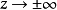时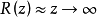，。此时等相位面也是平面。

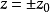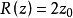时，。此时的等相位面半径最小。

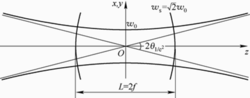
高斯光束的瑞利长度–当光束从束腰传播到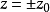处时，光束半径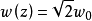，即光斑面积增大为最小值的两倍，这个范围称为瑞利范围，从束腰到该处的长度称为高斯光束的瑞利长度，通常记作f。

在实际应用中，一般认为基模高斯光束在瑞利长度范围内是近似平行的，因此也把瑞利距离长度称为准直距离。从瑞利长度表达式可以得出结论，高斯光束的束腰半径越小，其准直距离越长，准直性越好。

高斯光束的远场发散角–从高斯光束的等相位面半径以及光束半径的分布规律可以知道，在瑞利长度之外，高斯光束迅速发散，定义当时高斯光束振幅减小到最大值1/e处与z轴夹角为高斯光束的远场发散角（半角）：

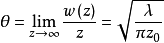
包含在全远场发散角内的光束功率占高斯光束总功率的86.5%。

高斯光束在轴线附近可以看成一种非均匀高斯球面波，在传播过程中曲率中心不断改变，其振幅在横截面内为一高斯分布，强度集中在轴线及其附近，且等相位面保持球面。

准直系统计算我们对于准直系统的计算，理论根据就是高斯光束的传输特性计算式.对于线度远大于输入光斑的透镜来讲，该输入光可视为点光源，其远场发散角就是该点光源的"边沿线"夹角；于是我们可根据透镜的具体参数，简单的用几何光学的方法计算该准直系统的光斑大小和最大工作距离.

意义而从高斯函数，我们可以计算当通光孔径多大时，光能的损失是多少，并不是通光区直径等于或略大于光斑直径时，光能就可以完全通过，事实上，此时的损耗高达0.6dB。简单的估计，是让通光直径是光斑的2倍或以上。3