[科普中国]-二次量子化

简单介绍

量子力学基本原理指出，描写全同粒子系统的态矢量，对于任意一对粒子的对调来说必须是对称的（玻色子系统）或反对称的（费米子系统）。全同粒子系统的理论具有很多独有的特点,人们根据这些特点发展了一种特殊的理论形式，这种使用产生算符和消灭算符在对称化的希尔伯特空间处理全同粒子系统的方法，通常称为二次量子化方法。

对称化的基矢全同粒子系统的最主要的特点是粒子的不可分辨性，即粒子不可以区分、不可以编号。但是为了作数学上的描述，粒子又必须编号。在对态矢量的模仿中，具有不同号码的粒子完全处于相同的地位，这样粒子虽然编了号，但仍是不可分辨的目的。1

可以把对称化和反对称化的基矢写成下式的形式，并统称之为对称化基矢。

只需对玻色子取，对费米子取即可。这一基矢描写的是在n个粒子中，有一个处于态，一个处于态的状态。由于已经对称化（以后用对称化一词兼代表反对称化），粒子的编号已无物理意义，因此左边的基矢符号中不出现粒子的编号。

对于玻色子系统，中可以有几个相等，而它们在基矢符号内的次序可以任意；对于费米子系统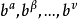，之间每对调一次，基矢要改变符号，因而这些b中不能有相同的，这正是泡利不相容原理的反映。

正交归一化关系和完全性关系正交归一化关系和完全性关系即称化基矢的正交归一化关系。根据这个关系，不同的基矢是正交的，但一个基矢与自己的内积并不全等于1，对于连续谱也不全等于函数，而有时是函数再乘一个常数。目前我们不想改变这个情况，因为一律改成1或函数反而不便。这种情况仍称之为归一化。

提出狄拉克曾把麦克斯韦的光关进一个盒子里，于是光的动态像一组振子。然后他给这种振子强加上量子性质。麦克斯韦的光理论是个波动理论，新的量子化理论实际上是包含波动和微粒两方面的一个理论，实际上指成群的光子。狄拉克的光理论的成功激发了人们的探索。海森堡和泡利.约尔当和魏格纳以及其他人，开始推广这个见解，把它应用到别的种类的波上，如薛定谔波和狄拉克电子波。虽然这两种波是量子波，它们既代表纯粹的波也代表粒子，但是想要修改这两种波是有充分理由的。所以理论家取各种各类的量子物质波，其中有狄拉克的电子波，将它看成仿佛是和麦克斯韦光波同等的“经典波”，用一种和狄拉克用于光波的手法原则上类似的手法，给物质波再强加上一些量子性质——这个程序称作二次量子化。

研究动机在多体系统中，对于处理全同粒子（identical particles），包括玻色子（bosons）和费米子（fermions）来说，理论上可以用Schrondinger方程去描述这系统。而波函数是各粒子位置或容间的波函数，玻色子和费米子都有相应的方法写出其波函数而符合其统计条件的。可是，处理这样的波函数太麻烦，而且若量子态的分布是连续的，处理起来十分麻烦。

因此，研究二次量子化，用升降算符（creation and annihilation operators）去描述，这样数学处理便容易得多，我们也知道怎样用这些算符去推演其他可观察物理量。另外，降算符相干态可用复数（玻色子）或Grassmann数（费米子）表示，数学工具都很齐备。

二次量子化步骤1、选择广义坐标，构造拉式量；

2、求出正则动量；

3、根据泊松括号得出对易关系；

4、转化到粒子数表象，引入湮没算符。

缺点二次量子化方法能够自然而简洁的处理全同粒子的对称性和反对称性，所以即使在粒子数守恒的非相对论多体问题中，也被广泛应用。

然而，二次量子化理论反映物质场的特征是不够全面的。其一：只用作为场的自由度的广义坐标，是一维的无穷多个指标的广义坐标，也就是说尽管是多个指标，它在空间的自由度却仅有一维。无穷多个指标的广义坐标，只分别对应无穷多个光量子，描写它们一维的状态。为了描写物质场的矢量性，物质场的自由度的广义坐标也应该是多维的广义坐标，必须把推广成对应物质场在处的振动的动量，对应物质波的几率密度，即传统的二次量子化理论中的态函数。2