概念
矢量耦合系数是两个角动量耦合时,它们的本征函数的组合系数。从数学的角度,克莱布什-戈登系数出现在紧李群的表示论中,它研究的是两个不可约表示的张量积如何分解成不可约表示的直和。克莱布什-戈登系数因阿尔弗雷德·克莱布什和保罗·哥尔丹而得名。1
基本原理对于由两个粒子组成的体系,用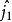 、
、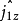 和
和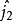 、
、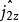 分别表示两个粒子的角动量算符和角动量的
分别表示两个粒子的角动量算符和角动量的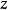 分量算符,
分量算符,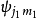 和
和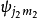 分别表示算符
分别表示算符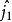 、
、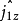 和
和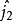 、
、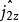 的共同本征函数。若以乘积
的共同本征函数。若以乘积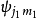
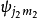 作为希耳伯空间的基矢,则这两个粒子相耦合的体系的波函数
作为希耳伯空间的基矢,则这两个粒子相耦合的体系的波函数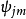 (它是算符
(它是算符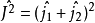 和
和 的共同本征函数)可以表达成:
的共同本征函数)可以表达成:
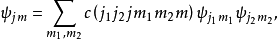 其中系数
其中系数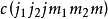 ,称为矢量耦合系数或克莱布什-戈登系数。
,称为矢量耦合系数或克莱布什-戈登系数。
以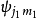
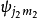 为希耳伯空间的基矢所构成的表象称为无耦合表象。以
为希耳伯空间的基矢所构成的表象称为无耦合表象。以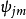 为希耳伯空间的基矢所构成的表象称为耦合表象。因此,矢量耦合系数也就是无耦合表象与耦合表象的基矢之间的幺正变换矩阵的矩阵元。
为希耳伯空间的基矢所构成的表象称为耦合表象。因此,矢量耦合系数也就是无耦合表象与耦合表象的基矢之间的幺正变换矩阵的矩阵元。
角动量 = 转动惯量 * 角速度其中,角动量和角速度是矢量,其方向按一般的约定是,与旋转轴相同,指向右手螺旋方向(右手握旋转轴,四指指向旋转方向,拇指向上方向为角动量和角速度矢量的方向)。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国