[科普中国]-全电流定律

定义全电流

一般情形下，通过空间某截面的电流应包括传导电流与位移电流，其和称全电流(total current) 。

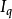假定为全电流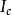， 为传导电流或运动电流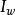，为位移电流：

（D为电通密度，S为截面面积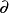， 表示偏微分符号，下同）

全电流是连续的，在空间构成闭合回路。导线中有传导电流（一般，导体中也有很小的位移电流），而电容器中有位移电流，即传导电流中断处，有位移电流接上。2

定律麦克斯韦将安培环路定理推广为全电流定律，可表示为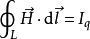： ，也即2

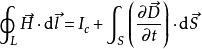
当闭合回线可分为几段，闭合回线的分段原则是：磁场强度相同，截面积相同，材料相同；而每段内H为常量，并和线段方向一致，沿闭合回线总磁压为各段磁压的代数和。这种情况下全电流定律又可表示为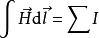

其中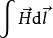， 是磁场强度矢量沿任意闭合线（常取磁通作为闭合回线）的线积分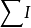； 是穿过闭合回线所围面积的电流代数和.

安培换路定律电流正负的规定：任意选定一个闭合回线的围绕方向，凡是电流方向与闭合回线围绕方向之间符合右螺旋定则的电流作为正，反之为负；在均匀磁场中，HL=IN，H=IN/L。

推导设真空中有一电荷+q，在X 轴正方向以速度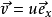 运动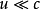（ ）。在t 时刻位置在A 处，如图1所示， 则该时刻，电荷+q在空间一点 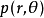所产生的磁场H可由毕奥-萨伐尔定律求得：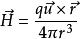

其中r是粒子到观察者的位置矢量。沿X轴方向看去，H的方向为顺时针方向，且以r与X轴夹θ角，旋转一周得到半径为R的闭合曲线C上各点的H大小相等。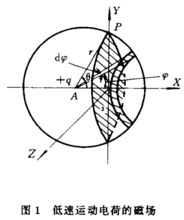

磁场强度H沿C顺时针方向一周的线积分为：

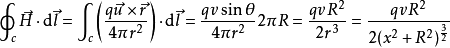
设s是y-z平面上以c为边界的圆面，则通过s面的位移电流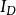 为：

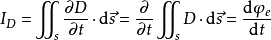
这里s不随时间变化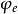， 是穿过s面的电通量。

由几何关系可知，通过s面的电通量是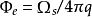 ，其中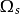 是s在粒子处所张立体角。可以求得：当x 0时，积分遍及 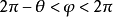， 则电通量是：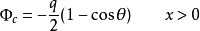

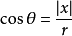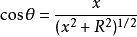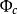以上两式符合相反表明：当粒子在左边时，电通量通过s面向右，而粒子在右边时，电通量通过s面向左。因 ，x 0 时， ，因此 可以写成：

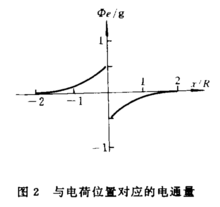
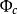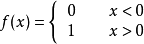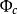注意到 在x=0处非连续，如图2所示。因而可用单位阶跃函数表示： ，因而 可以写成：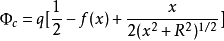

根据阶跃函数的性质，可求得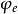 对时间的微商：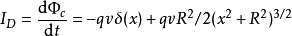

其中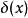 是狄拉克δ函数，此式对处在任意位置的粒子均成立。由此可求得磁场强度H沿C顺时针方向一周的线积分为：

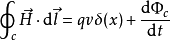
上式中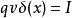 是粒子穿过s面的瞬时电流，这一点可以用下述方法推证。

考虑一线电荷密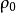度为 ，长度为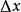 的带电棒，当 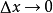时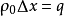， 保持不变，假定该棒以速度 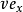沿x轴运动，当 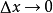时，该棒变成点电荷，其磁场强度由上式给出，当棒的中心处在原点的这一瞬间，沿x轴的线电荷密度是：

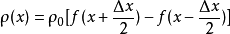
因而通过Y-Z平面的粒子电流即运流电流是

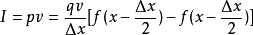
上式求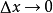时的极限即得

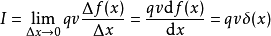
因而磁场强度H沿C顺时针方向一周的线积分可写成：

这就是全电流定律的表达式。1

讨论适用情况全电流定律既适用于电流恒定情况，又适用于非恒定情况。

对恒定情况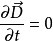， ，有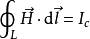

若所讨论的问题中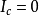， ，则磁场仅由位移电流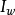（ ）产生（其磁场写作 ）

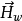即：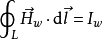

变化磁场电场对比如下两方程 ：

变化的电场产生磁场：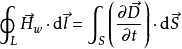

变化的磁场产生感应电场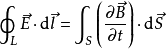： （B为磁通密度）

可见两方程非常对称。其不同点在于变化电场和产生的磁场之间为右手螺旋关系，变化磁场和感生电场之间为左手螺旋关系。

位移电流假说1.麦克斯韦提出假说：变化的磁场在其周围空间会激发一种涡旋状的非静电场强，称为涡旋电场。并以此为基础总结出了电场的环路定理。

2.对于稳恒电流，磁场满足安培环路定理：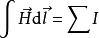

这个定理表明，磁场强度沿任意闭合回路的线积分等于穿过以该闭合回路为边界曲面的传导电流的代数和。但是，以闭合回路为边界的曲面原则上有无穷多个。也就是说，在稳恒电流情况下，对于以闭合回路为边界的所有曲面而言，安培环路定理总是成立的。但是，对于非稳恒电流，情况将不是这样的。

比如取电容器两极板间为一闭合的曲面，但是由于其中没有传导电流，所以安培环路定理右边为零；但是不在两极板间取的回路，明显电流和不是为零的，导致运用安培环路定理的时候出现了矛盾。

所以麦克斯韦大胆的提出假说：变化的电场能在其周围激发磁场。

并将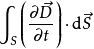 定义为位移电流，那么在上面讲的例子当中，取在两个极板之间的回路，再应用安培环路定理就是成立的了，但是此时等式右边的电流不是单独的传导电流，而是加上假说提出的位移电流。

正是如此，麦克斯韦进一步完善了他的电磁场理论，由此他毅然提出了全电流定理，以来完善安培环路定理的缺陷，就如上面的表述。

通过以上的研究，麦克斯韦完善了他的电磁场理论。3